Scaling Law 定义:随着模型大小、数据集大小和用于训练的计算浮点数的增加,模型的性能会有规律性的提高。并且为了获得最佳性能,所有三个因素必须同时放大。当不受其他两个因素的制约时,模型性能与每个单独的因素都有幂律关系(Power Law Relationship)。因此,当这种幂律关系出现时,我们可以提前对模型的性能进行预测。
Key Scaling Laws:
- 模型尺寸: LLM 的性能通常随着模型参数数量的增加而提升。
- 训练数据量: 随着训练数据量的增加,LLM 的性能也会提高。
- 训练时间: 训练时间越长,LLM 的性能通常越好。
- 训练硬件: 训练硬件的性能(例如 GPU 数量和速度)也会影响 LLM 的性能。
Scaling Law 的意义:
Scaling Law 对于理解和改进 LLM 至关重要,因为它提供了以下见解:
- 模型设计: Scaling Law 指导模型架构师选择最佳模型尺寸和参数数量以实现特定任务。
- 训练策略: Scaling Law 帮助研究人员确定最佳训练数据量和时间以最大化模型性能。
- 硬件选择: Scaling Law 告知研究人员和从业人员所需的训练硬件类型和规模以实现所需性能水平。
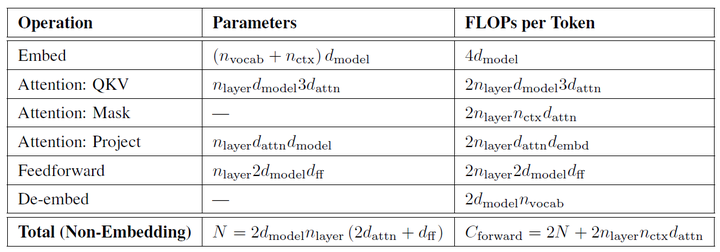
- 类似 GPT‑4 结构的模型估算方法,有浮点运算量(FLOPs)$C$、模型参数 $N$ 以及训练的 tokens 数 $D$ 之间的关系:$C \approx 6ND$
- 模型的最终性能主要与浮点运算量(FLOPs)$C$、模型参数 $N$ 以及训练的 tokens 数(训练数据量)$D$ 三者相关,而与模型的具体结构(层数/深度/宽度)在一阶上基本无关。
- 对于 $C$、$N$、$D$,当不受其他两个因素制约时,模型性能与每个因素都呈现幂律关系。
- 为了提升模型性能,$N$ 与 $D$ 需要协同放大,但最佳的放大比例取决于“计算预算目标”。
- Scaling Law 可推广到语言、视觉及多模态任务,但指数与最优点因任务/数据而异。
核心公式:
\[L(x)=L_{\infty}+(\frac{x_0}{x})^\alpha \\ \begin{align} L_\infty \approx S({True}) &&& \text{"Irreducible Loss"} \\ (\frac{x_0}{x})^{\alpha_x} \approx D_{KL}({True}||{Model}) &&& \text{"Reducible Loss"} \end{align} \\\]- 第一项$L_\infty$是指无法通过增加模型规模来减少的损失,可以认为是数据自身的熵(例如数据中的噪音);
- 第二项$(\frac{x_0}{x})^\alpha$是指能通过增加计算量来减少的损失,可以认为是模型拟合的分布与实际分布之间的差。
根据公式,增大 $x$(例如计算量 $C$),模型整体 loss 下降、性能提升;当 $x \to \infty$ 时,第二项逼近 0,整体趋向于 $L_\infty$。
其中以 GPT‑4、Baichuan‑2、MindLLM 为代表的 LLM 均在论文中指出符合这一 scaling law。
计算最优与 Chinchilla 法则(Compute‑Optimal)
实践中有两条常见“最优曲线”观点:
- OpenAI(Kaplan 等,早期):在固定计算预算下,更倾向“更大模型、较少数据”,经验指数常被引用为 $a\approx0.73, b\approx0.27$。
- DeepMind Chinchilla(Hoffmann 等,2022):提出“数据不足训练”的普遍性,主张在固定计算预算下应“更小模型、更多数据”,近似 $a\approx b\approx 0.5$,即 $N$ 与 $D$ 同阶扩展,更贴近 compute‑optimal。
两者并不矛盾:它们对应不同的数据可得性与目标函数。工业落地常以 Chinchilla 策略为基线,再按领域数据质量微调。
数据质量、去重与混合策略
Scaling 并非“只堆量”。数据质量、去重策略(near‑dup 去重)、域覆盖与指令分布会改变幂律常数与收敛速度。经验上:
- 在同等 tokens 下,高质量语料(代码/学术/高置信网页)能显著改善前期收敛;
- 混合配比需覆盖目标下游任务的语义分布,避免 domain shift 导致的“上限抬不动”;
- 指令数据(SFT)不直接改变预训练 scaling,但决定小计算量下的下游有效性。
Implement(实操)
根据幂律定律,模型参数固定时,无限堆数据并不能无限提升性能,最终会趋向某个上限。可按以下流程做 scaling law 试验与规划:
首先准备充足的数据(例如1T),设计不同模型参数量的小模型(例如0.001B - 1B),独立训练每个模型,每个模型都训练到基本收敛(假设数据量充足)。根据训练中不同模型的参数和数据量的组合,收集计算量与模型性能的关系。然后可以进一步获得计算效率最优时,即同样计算量下性能最好的模型规模和数据大小的组合,模型大小与计算量的关系,以及数据大小与计算量的关系。
根据 Baichuan 的实验,发现 $N_{opt} \propto C^a$,$D_{opt} \propto C^b$,即计算效率最优时,参数与数据相对计算量的幂次呈线性关系。由 $C=6ND$ 可得 $a+b=1$,但 $a,b$ 的具体取值存在分歧:OpenAI 倾向 $a\approx0.73,b\approx0.27$,而 DeepMind/Google 验证 $a\approx b\approx0.5$。
假设遵循计算效率最优来研发 LLM,那么根据 Scaling Law,给定模型大小可以推算最优计算量,进而推算所需 tokens 数。但需注意:计算效率最优针对的是训练阶段,不等价于推理最优;实际应用中常需要权衡推理成本(延迟/吞吐/显存)。
Meta 在 LLaMA 的观点是:给定目标性能,不必用最优计算效率在最短时间训练完;而是可在更大规模数据上训练一个相对更小的模型,从而在推理阶段获得更低成本。按 Scaling Law,10B 模型或许“理论上”只需 200B 数据,但在 1T 级数据上 7B 模型仍能继续涨点,这反映了数据质量/多样性对上限的影响。
所以LLaMA工作的重点是训练一系列语言模型,通过使用更多的数据,让模型在有限推理资源下有最佳的性能。
具体而言,确定模型尺寸后,Scaling Law 给出的是一条“推荐数据量—计算量”的曲线。实际训练中应监控验证集困惑度、下游任务指标的增长趋势;只要仍有显著收益,就可以继续增加数据与训练步数。
常见误解与注意事项
- 并非“只要加大就一定更好”:幂律只在一定范围内成立;当数据噪声/分布不当、优化器与学习率不匹配时,会提前遇到收益递减。
- “结构无关”并非绝对:架构/激活/归一化会改变幂律的常数项与可达上限,影响实际最优点。
- 评估要贴近目标:用困惑度趋势判断 scaling 足够,但业务落地需要同时跟踪下游任务表现与推理成本。
结语
Scaling Law 提供了“算力—参数—数据”的量化刻度尺。结合 compute‑optimal 策略、数据质量工程与面向推理的资源约束,才能在真实场景中把幂律收益转化为稳定、可复现的模型增益。
