随着 Deep Neural Networks(DNNs)的广泛落地,如果始终使用体量巨大的模型,会对算力与存储提出很高要求。因此,围绕“压缩与加速”的系统化方法被广泛采用,尤其是在端侧/边缘推理中,带来如下优势:
- 减轻服务器端计算压力,支持云边协同的负载均衡;
- 实时性更好,端上响应更快;
- 稳定性与可用性更高;
- 隐私更友好,数据不必出端。
“压缩”(减少参数/存储)与“加速”(降低计算/延迟)并非同一概念,但常互相促进:量化和结构化剪枝既能降存,也能提速。整体来看常分三个层次:
- 算法层:量化与定点化、模型剪枝、低秩/分解、紧致算子(DW/GroupConv)、知识蒸馏等;
- 编译/框架层:图优化与算子融合、内存复用、稀疏库、指令级优化(NEON/SIMD);
- 硬件层:GPU/CPU/NPU/FPGA/ASIC 上的张量核、稀疏加速与带宽优化。
压缩与加速全景(速览)
- 量化(Quantization):PTQ/QAT,per‑tensor vs per‑channel,对称/非对称,整型推理(INT8/INT4);
- 剪枝(Pruning):非结构化 vs 结构化,N:M 稀疏(如 2:4),通道/层级剪枝与重训练;
- 低秩/分解(Low‑rank/Tensor Decomp):SVD、CP/Tucker、分解卷积核与 1×1 瓶颈;
- 蒸馏(Distillation):响应蒸馏(logit/soft target)、特征/注意力蒸馏、在线/自蒸馏;
- 框架/编译:TensorRT、ONNX Runtime、TVM、XLA 的图优化与算子融合;
- 评估:精度跌落预算、延迟/吞吐、峰值/常驻显存、功耗与成本。
简单总结一下常被提及的四种方法:
| Theme Name | Description | Application | More Details | Drawback |
|---|---|---|---|---|
| 参数剪枝和共享(Parameter Pruning and Sharing) | 减少对性能不敏感的冗余参数 | 卷积层和全连接层 | 对不同设置有鲁棒性,能够实现好的性能,能支持脚本(Scratch)和预训练模型的训练 | 1)量化和二进制:二进制网络的精度损失比较大;2)剪枝和共享:更难以收敛,要微调参数,不够灵活;3)设计结构矩阵:结构矩阵会伤害到模型性能,且结构矩阵不好找。 |
| 低秩分解(Low-rank factorization) | 使用矩阵/张量分解去估计有信息量的参数 | 卷积层和全连接层 | 标准的管道(pipeline),容易执行,能够支持脚本和预训练模型。 | 1)分解的操作不易执行,其计算消耗是昂贵的;2)当前的算法时逐层进行的,因此不能全局压缩;3)分解后,模型的收敛难度增加。 |
| 转移/紧致卷积滤波器(Transferred/compact convolutional filters) | 设计特殊结构的卷积滤波器去保存参数 | 卷积层 | 算法依赖于应用,通常实现好的性能,只支持脚本中训练 | 1)只支持宽的神经网络而不支持深度的神经网络;2)转移的假设性太强导致某情况的结构不太稳定。 |
| 知识蒸馏(Knowledge distillation) | 通过大模型中蒸馏知识训练一个紧致的神经网络 | 卷积层和全连接层 | 模型的性能对应用是敏感的并且网络结构只支持从脚本中训练 | 1)目前知识蒸馏只支持softmax损失的分类模型;2)与其他方法相比,模型假设太严格了。 |
Parameter Pruning and Sharing
Quantization and Binarization
量化通过减少表示权值/激活的比特宽度来压缩模型与加速推理。极端情形是 1‑bit(二值网络)。也可使用权值聚类(weight clustering)以共享中心值,进一步降低存储。常见实践:
- PTQ(后训练量化)与 QAT(量化感知训练);
- per‑tensor 与 per‑channel 量化;对称/非对称零点;
- 线性量化与对数量化;激活动态范围校准;
- INT8 为工程常用折中,INT4/FP8 需更精细训练与校准。
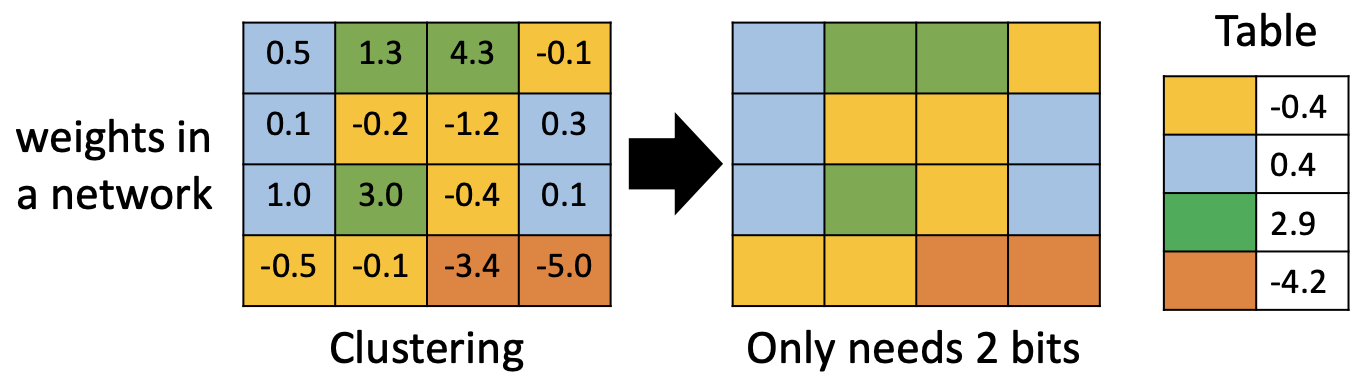
注意:二值/超低比特精度损失显著;不同硬件对 INT8/FP8 的支持差异较大,需要结合部署目标选择方案。
Pruning and Sharing
剪枝的基本思想是移除不重要的权重或结构(通道/层),得到稀疏或更紧凑的网络。重要性可由权值幅度、敏感度、BN 缩放系数、梯度/海森近似等估计。通常采用“逐步剪枝 + 微调”的流程,以减小精度损失;结构化剪枝(通道/卷积核/层)更易获得实际加速。
网络剪枝和共享已经被用于减少网络复杂性和处理过拟合任务。一个早些的剪枝方法是基于权值的。最优脑损害(The Optimal Brain Damage)和最优脑外科医生(the Optimal Brain Surgeon)方法减少了基于损失函数Hessian阵的连接层的参数,这些工作说明这样的剪枝得到了较高的精确率比那些基于权值剪枝方法的机制。
这个方向的最近趋势是剪枝冗余性,即预训练CNN模型中非信息的权值。
训练期可引入稀疏正则((\ell_1/\ell_0) 近似、Group‑Lasso)或采用 N:M 稀疏(如 2:4)以对齐硬件稀疏加速能力。
注意:非结构化稀疏对通用硬件提速有限;过度剪枝会导致不可逆的精度退化;需要稳定的微调与校准流程。
Designing Structural Matrix
在包含全连接层的结构中,探索全连接层中的参数冗余性时很重要的,这总是内存消耗的瓶颈。全连接网络层一般是$f(x, M)=\sigma(Mx)$,这里的$\sigma(\cdot)$是一个元素式的非线性操作,$x$是输入向量,和$M$是$m \times n$的参数矩阵。其中$M$通常是大的稠密矩阵,计算矩阵向量乘法的时间复杂度是$O(mn)$。因此,一个直觉上的剪枝方法是利用$M$作为一个参数化的结构矩阵。一个$m \times n$矩阵可以描述成一个使用少于$mn$参数的矩阵去呼叫一个结构矩阵。典型上,结构不应该只减少内存消耗,也急剧的大叔了推理和训练阶段,如果通过快速矩阵向量乘法和梯度计算。
在这个方向上,有一些研究提出了简单而有效的基于循环投影的方法,同时维持的可竞争的错误率。给定一个向量$r=(r_0, r_1,…,r_{d-1})$,一个循环矩阵$R \in R^{d \times d}$定义如下:
\[R=circ(r) := \begin{bmatrix} r_0 & r_{d-1} & \cdots & r_2 & r_1 \\ r_1 & r_0 & r_{d-1} & & r_2 \\ \vdots & r_2 & r_0 & \ddots & \vdots \\ r_{d-2} & & \ddots & \ddots & r_{d-1} \\ r_{d-1} & r_{d-2} & \cdots & r_1 & r_0 \\ \end{bmatrix}\]这样,内存消耗就会从$O(d^2)$变成$O(d)$. 而且训练矩阵也能够使用快速傅里叶变换加速矩阵计算。给定一个$d$维的向量$r$,则$Rr$乘法的时间复杂度维$O(d log(d))$
缺点:这个方法的一个问题是结构约束将会损害性能,由于约束会带给模型偏移。另一方面,找一个合适的结构矩阵是困难的,目前也没有理论告诉我们怎么做。
Low-Rank Factorization and Sparsity
卷积操作占据了深度CNNs模型中的最大计算篇幅,因此减少卷积层能够提升压缩率同时也能加快运算速度。对于卷积核,它可以被认为一个4D张量。基于张量分解的想法驱使我们本能的认为4D张量的冗余性去除会有一个显著提升,这是一个特殊的方式去移除冗余性。注意到全连接层,它能够被视为一个2D矩阵并且低秩也能有所帮助。
长期以来,人们使用低秩滤波器加速卷积:例如用高维 DCT/小波基通过张量积构造可分滤波器,或用 SVD/CP/Tucker 分解卷积核张量以分解为多层/逐维卷积(如 k×k → k×1 + 1×k)。
低秩估计通常逐层进行:分解后冻结该层并基于重构误差/验证集微调。CP 分解常用非线性最小二乘求解,但病态性强,最优 rank‑K 未必存在,需要经验选择秩并配合重训练。
正如前面所提,全连接层可以看成是2D矩阵,因此上述的方法(指低秩估计的方法)也能够应用到这儿(指全连接层的分解)。也有工作应用截断奇异值分解去分解全连接层用于设计紧凑的多任务深度学习框架。
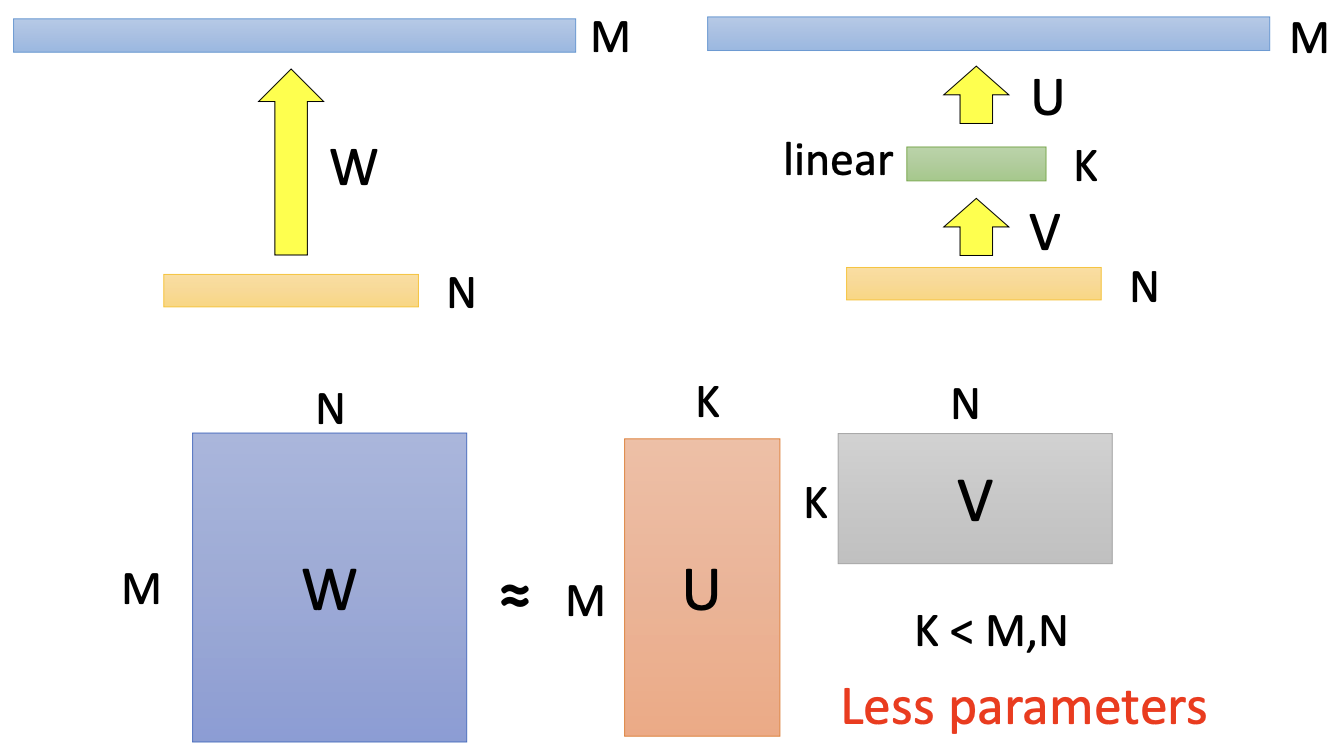
缺点:低秩方法在估计矩阵压缩和加速上是简单直接的。这个想法最近补充深度学习的优点,比如dropout, rectified units 和 maxout. 然而, 由于它涉及到分解操作,执行起来并不容易。分解是计算代价昂贵的。 另一个问题是当前的低秩估计方法是逐层的,因此不能执行全局的参数压缩, 而这对于不同的层保持不同的信息时重要的。最后,比较原始模型, 分解需要额外的再训练去实现收敛。
Transferred/Compact Convolutional Filters
CNNs 具有对平移/旋转等变换的稳健性。利用“等价性”思想,可将大卷积核表示为对一组基础滤波器施加可学习/确定的变换,从而复用参数并达到压缩目的。设输入为 (x),层为 (\Phi(\cdot)),变换为 (\tau(\cdot)),有:
\[\tau^{'} \Phi(x) = \Phi(\tau x)\]若满足 (\tau’\Phi(x)=\Phi(\tau x)),则可在滤波器空间复用/生成卷积核。经验上,对于宽网络(如 VGG 系列)更有效;在深且窄的网络(如 ResNet/GoogLeNet)上收益有限。
在这个方向,有许多最近的研究工作去建立一个由基础滤波集合构建的卷积层。(就是从不同的角度定义函数$\tau(\cdot)$
注意:过强的变换约束会引入偏置,影响泛化;需要结合具体骨干与部署目标权衡。
使用一个紧致的卷积滤波器能够直接减少计算损失。这个关键的想法是去替代松弛和过参数滤波器维紧凑的块进行加速,这能够显著的加速CNNs在一些基准上。
Knowledge Distillation
最早的知识转移工作可追溯至 Caruana 等。现代“知识蒸馏”(Knowledge Distillation)将大型教师模型的“软标签/特征/注意力”转移给小学生模型:先训练教师,再用教师输出指导学生。蒸馏可用于分类、检测、分割与生成建模(不止 softmax 分类)。
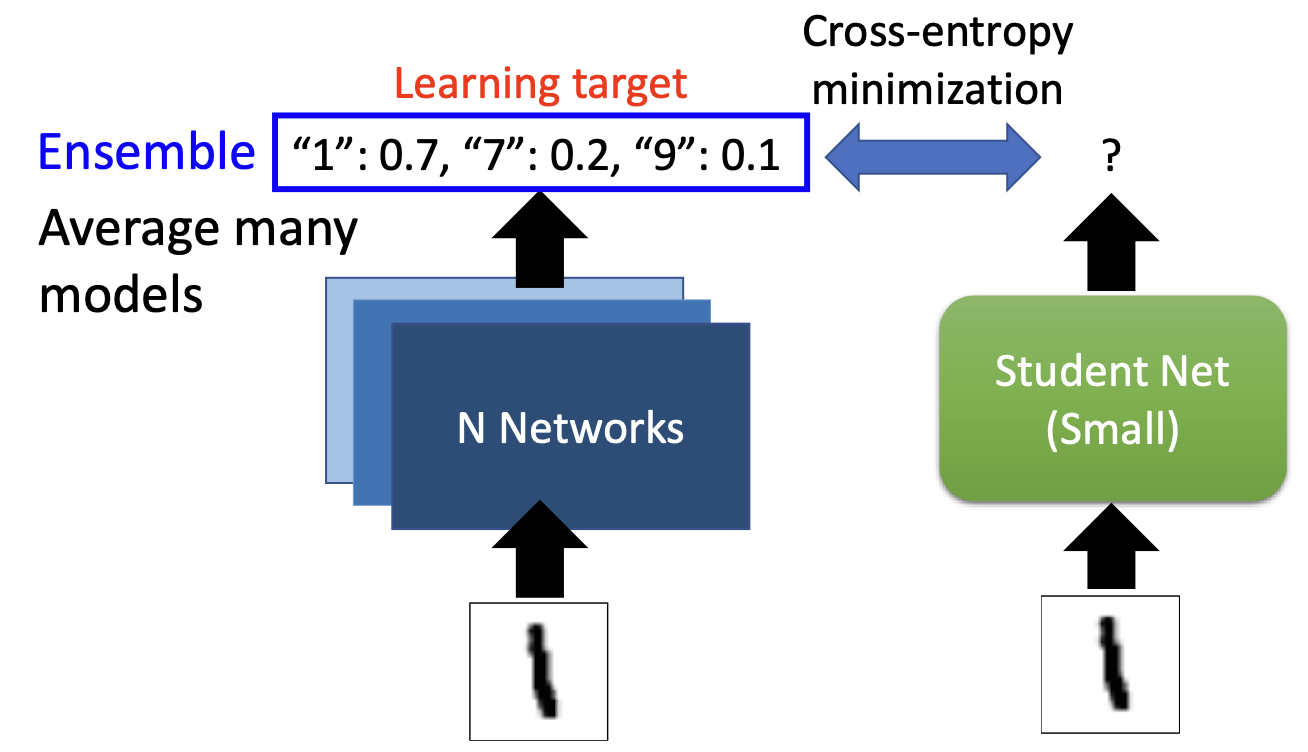
常见做法是温度 softmax:
\[y_i'=\frac{\exp(y_i/T)}{\sum_j \exp(y_j/T)}\]注意:仅用 logit 蒸馏可能导致风格过拟合;建议结合特征层蒸馏、数据增广与合成数据(如自蒸馏/在线蒸馏)以提高稳定性与适用范围。
评估流程与实践清单
- 指标:Top‑1/Top‑5、mAP/mIoU、延迟(P50/P95)、吞吐、功耗、显存;
- 流程:基线校准 → 候选方案对比(量化/剪枝/分解/蒸馏)→ 组合策略 → 回归测试与 A/B → 压测与稳定性;
- 落地工具:TensorRT、ONNX Runtime(EP)、OpenVINO、TVM、XLA、CoreML、TFLite;
- 工程位点:算子融合、内存复用、分页 KV/张量复用、批处理/连续批处理、并行度调度;
- 风险与排错:量化溢出/饱和、校准失配、BN 统计漂移、稀疏加载失败、编译器回退慢路径。
