Meta 的 Llama 2 是当前开源生态里可作为效果标杆的一类 LLM。虽未开放完整训练细节,但其公开的模型结构与推理实践具有很高的参考价值。
1 - Intro
2 - Process
关于通用的LLM对于文本的处理一般是以下流程:
输入数据:LLM的输入数据是一段文本,可以是一个句子或一段话。文本通常被表示成单词或字符的序列。
[君不见黄河之水天上来,奔流到海不复回。君不见高堂明镜悲白发,朝如青丝暮成雪。...五花马、千金裘,呼儿将出换美酒,与尔同销万古愁]
Tokenization:之后需要将文本进行Tokenization,将其切分成单词或字符,形成Token序列。之后再将文本映射成模型可理解的输入形式,将文本序列转换为整数索引序列(这个索引就是单词或字符在语料库中的index),这个过程通常由一些开源的文本 Tokenizer 工具,如 sentencepiece 等来处理
序列化->
['BOS','君','不','见','黄','河','之','水','天','上','来',',' ,'奔','流','到'...'与','尔','同','销','万','古','愁','EOS']
假设语料库索引化->
['BOS','10','3','67','89','21','45','55','61','4','324','565' ,'789','6567','786'...'7869','9','3452','563','56','66','77','EOS']
Embedding:文本信息经过Tokenization之后变成了 token 序列,而 Embedding 则继续将每个 Token 映射为一个实数向量,为 Embedding Vector。
'BOS'-> [p_{00},p_{01},p_{02},...,p_{0d-1}]
'10' -> [p_{10},p_{11},p_{12},...,p_{1d-1}]
'3' -> [p_{20},p_{21},p_{22},...,p_{2d-1}]
...
'EOS'-> [p_{n0},p_{n1},p_{n2},...,p_{nd-1}]
位置编码:对于Token序列中的每个位置,添加位置编码(Positional Encoding)向量,以提供关于Token在序列中位置的信息。位置编码是为了区分不同位置的Token,并为模型提供上下文关系的信息。
[p_{00},p_{01},p_{02},...,p_{0d-1}] [pe_{00},pe_{01},pe_{02},...,pe_{0d-1}]
[p_{10},p_{11},p_{12},...,p_{1d-1}] [pe_{10},pe_{11},pe_{12},...,pe_{1d-1}]
[p_{20},p_{21},p_{22},...,p_{2d-1}] + [pe_{20},pe_{21},pe_{22},...,pe_{2d-1}]
... ...
[p_{n0},p_{n1},p_{n2},...,p_{nd-1}] [pe_{n0},pe_{n1},pe_{n2} ,...,pe_{nd-1}]
Transformer :在生成任务中,以llama为代表的类GPT结构的模型只需要用到Transformer 的decoder阶段,即Decoder-Only。
自回归生成:在生成任务中,使用自回归(Autoregressive)方式,即逐个生成输出序列中的每个Token。在解码过程中,每次生成一个Token时,使用前面已生成的内容作为上下文,来帮助预测下一个Token。
model = LLaMA2()
def generate(inputs, n_tokens_to_generate):
for _ in range(n_tokens_to_generate):
# auto-regressive decode loop
output = model(inputs)
# model forward pass
next = np.argmax(output[-1])
# greedy sampling
inputs.append(next)
# append prediction to input
return inputs[len(inputs) - n_tokens_to_generate :]
# only return generated tokens
input = [p0, p1,p2]
#对应['BOS','君','不']
output_ids = generate(input, 3)
# 假设生成 ['p3','p4','p5']
output_ids = decode(output_ids)
# 通过Tokenization解码
output_tokens = [vocab[i] for i in output_ids]
# "见" "黄" "河"
输出处理:生成的Token序列通过一个输出层,通常是线性变换加上Softmax函数,将每个位置的概率分布转换为对应Token的概率。根据概率,选择概率最高的Token或者作为模型的预测结果。或者其他的的方法生成next token ,比如:
def sample_top_p(probs, p):
# 从给定的概率分布中采样一个token,
# 采样的方式是先对概率进行排序,然后计算累积概率,
# 然后选择累积概率小于p的部分,
# 最后在这部分中随机选择一个token。
probs_sort, probs_idx = torch.sort(probs, dim=-1, descending=True)
# 给定的概率降序排序
probs_sum = torch.cumsum(probs_sort, dim=-1)
# 从第一个元素开始,依次将序列中的每个元素与前面所有元素的和相加得到的
mask = probs_sum - probs_sort > p
probs_sort[mask] = 0.0
# 将累计和减去当前值>p的地方全部置0,留下来的就是概率较大的
probs_sort.div_(probs_sort.sum(dim=-1, keepdim=True))
# 归一化下
next_token = torch.multinomial(probs_sort, num_samples=1)
# 从归一化之后的样本抽取一个样本
next_token = torch.gather(probs_idx, -1, next_token)
# 从原始probs_idx找到next_token所对应的index
return next_token
3 - Architecture
Llama 系列这样的主流 LLM 常常沿用 GPT 结构,基于 Transformer 来构建。生成式任务根据给定输入序列的上下文预测下一个 token,因此通常只使用 Transformer 的 Decoder 部分;相较 Encoder,Decoder 在计算 Q·K^T 时引入因果 Mask,确保当前位置只关注已生成内容。
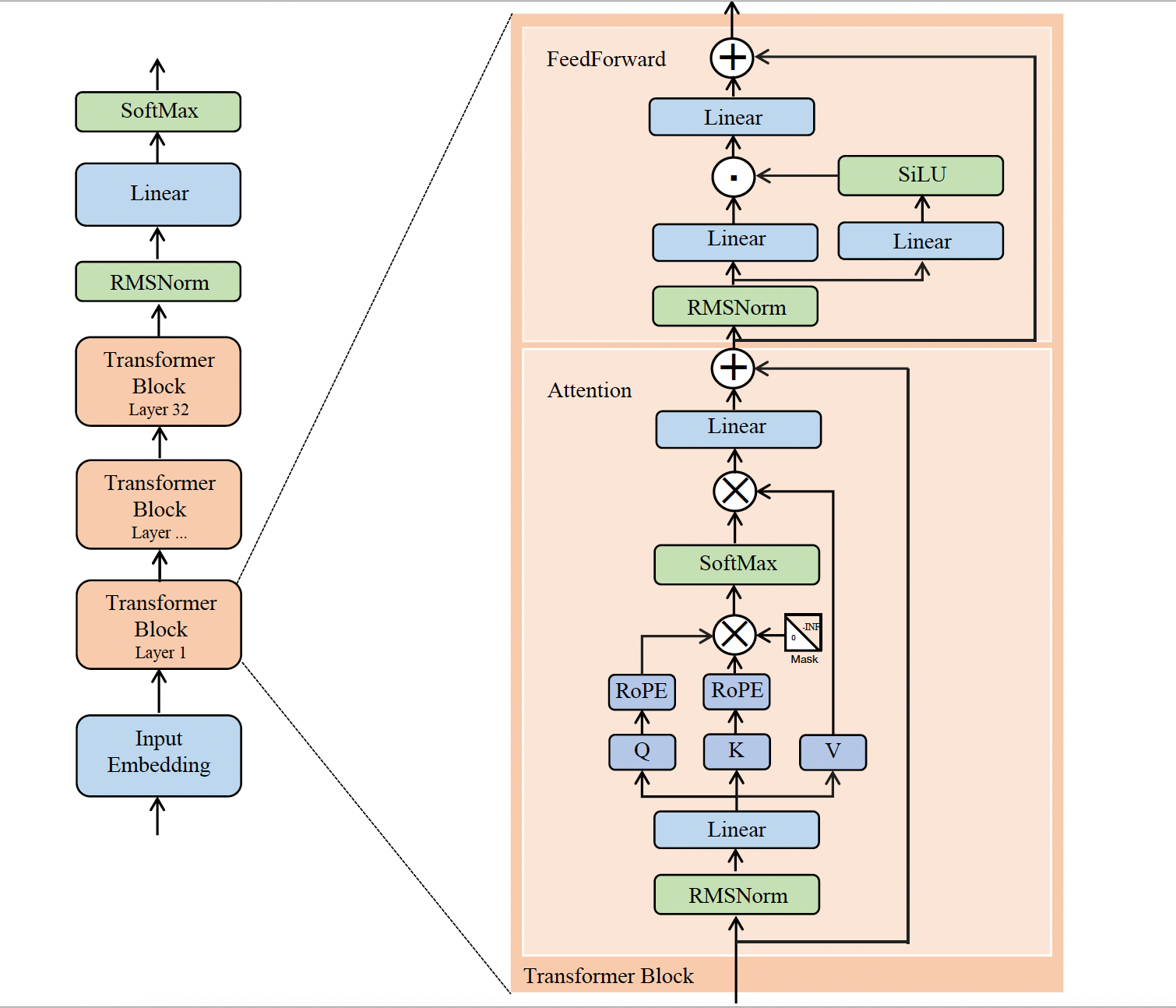
Llama2主要由32个 Transformer Block 组成,不同之处主要包括以下几点:
- 前置的RMSNorm层;
- Q 在与 K 相乘之前先使用 RoPE 进行位置编码;
- KV Cache,并采用 Group Query Attention;
- FeedForward层。
3.1 - RMSNorm
Transformer中的Normalization层一般都是采用LayerNorm来对Tensor进行归一化,LayerNorm可以被表达成:
\[y =\frac{x-E[x]}{\sqrt{Var[x]+\epsilon}}*\gamma+\beta \\ E[x] =\frac{1}{N}\sum^N_{i=1}x_i \\ Var[x] =\frac{1}{N}\sum^N_{i=1}(x_i-E[x])^2\]而RMSNorm则是LayerNorm的变体,省去了求均值过程,也没有了求偏置$\beta$,即:
\[y =\frac{x}{\sqrt{Mean(x^2)+\epsilon}}*\gamma \\ Mean(x^2) =\frac{1}{N}\sum^N_{i=1}x^2_i\]其中$\beta$和$\gamma$为可学习参数
# RMSNorm
class RMSNorm(torch.nn.Module):
def __init__(self, dim: int, eps: float = 1e-6):
super().__init__()
self.eps = eps # ε
self.weight = nn.Parameter(torch.ones(dim)) #可学习参数γ
def _norm(self, x):
# RMSNorm
return x * torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps)
def forward(self, x):
output = self._norm(x.float()).type_as(x)
return output * self.weight
3.2 - RoPE(Rotary Positional Encoding)
在通用LLM中,为了强调各个token的位置信息被传入计算attention中,往往将每个token的位置信息以position embedding的形式被编码进实际的input sequence idx中。
我们知道输入数据经过tokenization之后,会得到一组单词索引序列${w_0, w_1, w_2, … w_n }$,之后经过embedding处理后也就变成了${x_0, x_1, x_2, … x_n }$,embedding后的序列通过Linear层将输入数据$x_i$转换为对应的$q_i,k_i,v_i$,之后 便会对$q_i,k_i$两者做RoPE位置编码,之后便计算Attention。
其中 $x_i$ 为第 $i$ 个单词所对应的 $d$ 维词嵌入向量 ${x_{i_0}, x_{i_1}, x_{i_2}, … , x_{i_{d-1}} }$。
在标准的transformer中,通常是在整个网络进入Transformer Block之前做一个位置编码。
表达方式即$p_{i,2t}$表示第$i$个嵌入向量$x_i$的第$2t$,即偶数位个位置的位置编码:
\[\begin{align} f_{\{q,k,v\}}(x_i, i) & = W_{\{q,k,v\}}(x_i+p_i) \nonumber \\ p_{i, 2t} & = \sin (\frac{i}{10000^{\frac{2t}{d}}}) \nonumber \\ p_{i, 2t+1} & = \cos (\frac{i}{10000^{\frac{2t}{d}}}) \nonumber \end{align}\]与绝对位置编码相比,RoPE的引入是为了通过绝对位置编码的方式实现相对位置编码,其实用之处在于可以拓展到线性Attention中,这一特性使得RoPE在处理长文本任务中具有显著优势。同时随着文本位置的增加,RoPE旋转位置编码的影响力逐渐减弱。这种特性使得模型在关注重要信息时,能够减少冗余信息的干扰。RoPe通过模拟旋转矩阵来实现对序列中每个位置的编码。
3.2.1 - RoPE的数学原理
为了实现上述目的,通过下列运算给$q$和$k$添加了绝对位置信息:
\[\hat{q}_m=f_q(x_m, m) \\ \hat{k}_n=f_k(x_n, n)\]也就说经过上述函数处理,使得$\hat{q}_m,\hat{k}_n$为带有位置$m,n$的绝对位置信息。之后Attention会对$\hat{q}_m,\hat{k}_n$进行内积运算,所以希望经过上述函数处理之后,$\hat{q}_m,\hat{k}_n$在进行内积时能带入$m-n$这个相对位置信息,即满足$<f_q(x_m, m), f_k(x_n, n)> = g(x_m, x_n, m - n)$。
其中$f_q(x_m, m)$和$f_k(x_n, n)$是待求解的函数,$<>$符号表示求内积操作,而对于$g(x_m, x_n, m - n)$,我们只需要其表达式中含有$(x_m, x_n, m - n)$即可,或者说$\hat{q}_m$和$\hat{k}_n$内积的值受到$(m-n)$的影响。
关于$f()$的求解可以详见博文Transformer升级之路:2、博采众长的旋转式位置编码以及RoPE论文原文ROFORMER: ENHANCED TRANSFORMER WITH ROTARY POSITION EMBEDDING,以及一文看懂 LLaMA 中的旋转式位置编码(Rotary Position Embedding) ,总之得到结果:
\[f_q(x_m, m)=(W_qx_m)e^{im\theta} \\ f_k(x_n, n)=(W_kx_n)e^{in\theta}\]带入$g$可以得到:
\[\begin{align} g(x_m, x_n, m - n) & = <f_q(x_m, m), f_k(x_n, n)> \nonumber \\ & = Re[(W_qx_m)(W_kx_n)^*e^{i(m-n)\theta}] \nonumber \end{align}\]其中$Re$表示复数的实部,$(W_kx_n)^*$表示$(W_kx_n)$的共轭复数。也就是让$\hat{q}_m$和$\hat{k}_n$内积的值受到$(m-n)$的影响。根据欧拉公式$e^{ix}=\cos(x)+i\sin(x)$代入$f_q(x_m,m)$,有$f_q(x_m,m)=(W_qx_m)e^{im\theta}=(W_qx_m)[\cos(m\theta)+i\sin(m\theta)]$。
假设当前是2维平面即$d=2$,那么展开上述等式可以有:
\[\begin{align} f_q(x_m,m) & = (W_qx_m)[\cos(m\theta)+i\sin(m\theta)] \nonumber \\ & = (\begin{array}{cc|r} W^{11}_q & W^{12}_q \\ W^{21}_q & W^{22}_q\end{array})(\begin{array}{cc|r} x^{(1)}_m \\ x^{(2)}_m\end{array})[\cos(m\theta) + i\sin (m\theta)] \\ & =(q^{(1)}_m, q^{(2)}_m)[\cos(m\theta) + i\sin (m\theta)] \end{align}\]如果进一步将$(q^{(1)}_m, q^{(2)}_n)$这个向量用复数形式表示,即$(q^{(1)}_m+iq^{(2)}_n)$,代入后得到:
\[\begin{align} f_q(x_m, m) & = (q^{(1)}_m, q^{(2)}_n)[cos(m\theta) + i\sin(m\theta)] \\ & = (q^{(1)}_m+iq^{(2)}_n)(cos(m\theta) + i\sin(m\theta)) \\ & = [q^{(1)}_m\cos(m\theta) - q^{(2)}_m \sin(m\theta)] + i[q^{(1)}_m \sin(m\theta) + q^{(2)}_m\cos(m\theta)] \end{align}\]转换为向量的表达形式:
\[\begin{align} f_q(x_m, m) & = [q^{(1)}_m\cos(m\theta) - q^{(2)}_m \sin(m\theta)] + i[q^{(1)}_m \sin(m\theta) + q^{(2)}_m\cos(m\theta)] \\ & = [q^{(1)}_m\cos(m\theta) - q^{(2)}_m \sin(m\theta)], \; i[q^{(1)}_m \sin(m\theta) + q^{(2)}_m\cos(m\theta)] ] \\ & = (\begin{array}{cc|r}\cos (m\theta) & -\sin (m\theta) \\ \sin (m\theta) & \cos (m\theta)\end{array})(\begin{array}{cc|r} q_m^{(1)} \\ q_m^{(2)}\end{array}) \end{align}\]同理key部分也可以表示为:
\[f_k(x_n,n) = (\begin{array}{cc|r}\cos (n\theta) & -\sin (n\theta) \\ \sin (n\theta) & \cos (n\theta)\end{array})(\begin{array}{cc|r} k_n^{(1)} \\ k_n^{(2)}\end{array})\]其中,$\theta$是由位置$p$确定的旋转角度。在RoPe中,旋转角度$\theta$通常是位置$p$的函数,例如$\theta = \frac{p}{\sqrt d}$,$d$是维度。
3.2.2 - 多维空间的拓展
而对于多维词嵌入向量而言,即$d>2$的情况,同样可以通过,两两一组的方式来实现这种机制,即

这就是整个整个RoPE在位置编码时所作的工作,可以发现 $R_d_{\theta,m}$ 是一个稀疏矩阵,这样直接对$q,k$进行矩阵乘法的位置编码会很低效,所以可以通过以下方法来实现RoPE。
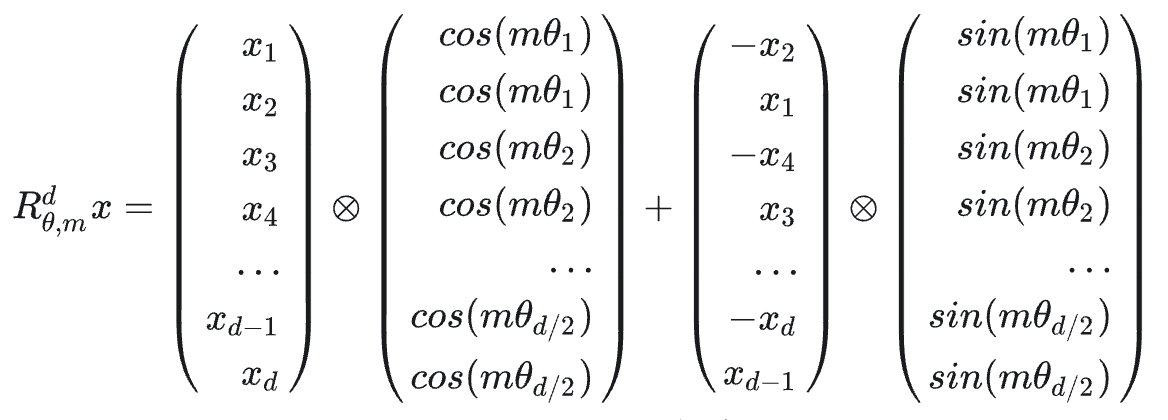
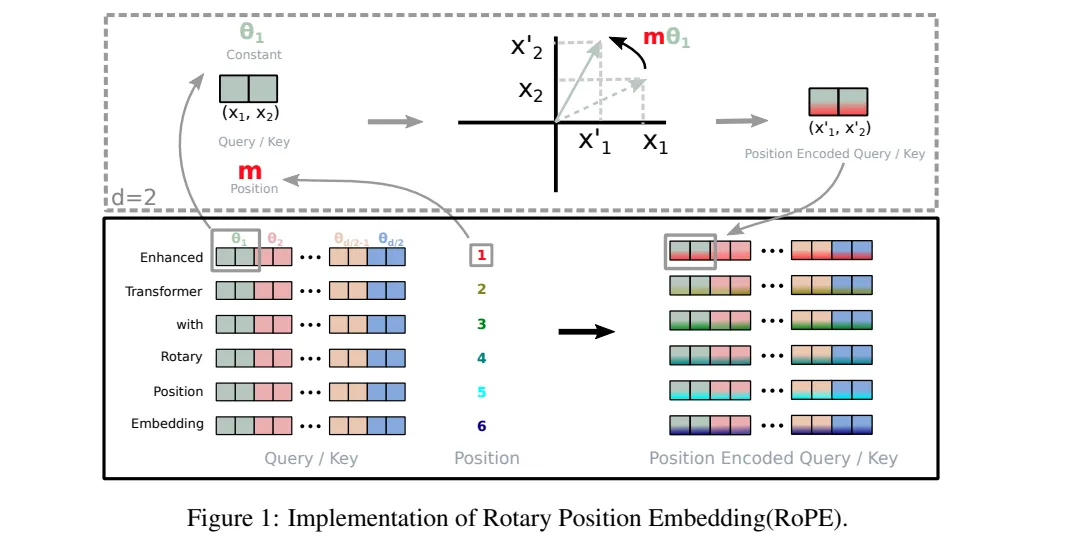
论文也提供了一个非常直观的图来说明RoPE的处理过程,如下所示, 序列两两一对利用复数坐标嵌入位置信息。
3.2.3 - RoPE Code
def precompute_freqs_cis(dim: int, end: int, theta: float = 10000.0):
# 计算词向量元素两两分组以后,每组元素对应的旋转角度
# arange生成[0,2,4...126]
freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
# t = [0,....end]
t = torch.arange(end, device=freqs.device) # type: ignore
# t为列向量 freqs为行向量做外积
# freqs.shape = (t.len(),freqs.len()) #shape (end,dim//2)
freqs = torch.outer(t, freqs).float() # type: ignore
# 生成复数
# torch.polar(abs,angle) -> abs*cos(angle) + abs*sin(angle)*j
freqs_cis = torch.polar(torch.ones_like(freqs), freqs) # complex64
# freqs_cis.shape = (end,dim//2)
return freqs_cis
def reshape_for_broadcast(freqs_cis: torch.Tensor, x: torch.Tensor):
# ndim为x的维度数 ,此时应该为4
ndim = x.ndim
assert 0 <= 1 < ndim
assert freqs_cis.shape == (x.shape[1], x.shape[-1])
shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)]
# (1,x.shape[1],1,x.shape[-1])
return freqs_cis.view(*shape)
def apply_rotary_emb(
xq: torch.Tensor,
xk: torch.Tensor,
freqs_cis: torch.Tensor,
) -> Tuple[torch.Tensor, torch.Tensor]:
# xq.shape = [bsz, seqlen, self.n_local_heads, self.head_dim]
# xq_.shape = [bsz, seqlen, self.n_local_heads, self.head_dim//2 , 2]
# torch.view_as_complex用于将二维向量转换为复数域 torch.view_as_complex即([x,y]) -> (x+yj)
# 所以经过view_as_complex变换后xq_.shape = [bsz, seqlen, self.n_local_heads, self.head_dim//2]
xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))
xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))
freqs_cis = reshape_for_broadcast(freqs_cis, xq_) # freqs_cis.shape = (1,x.shape[1],1,x.shape[-1])
# xq_ 与freqs_cis广播哈达玛积
# [bsz, seqlen, self.n_local_heads, self.head_dim//2] * [1,seqlen,1,self.head_dim//2]
# torch.view_as_real用于将复数再转换回实数向量, 再经过flatten展平第4个维度
# [bsz, seqlen, self.n_local_heads, self.head_dim//2] ->[bsz, seqlen, self.n_local_heads, self.head_dim//2,2 ] ->[bsz, seqlen, self.n_local_heads, self.head_dim]
xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3)
xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3)
return xq_out.type_as(xq), xk_out.type_as(xk)
# 精简版Attention
class Attention(nn.Module):
def __init__(self, args: ModelArgs):
super().__init__()
self.wq = Linear(...)
self.wk = Linear(...)
self.wv = Linear(...)
self.freqs_cis = precompute_freqs_cis(dim, max_seq_len * 2)
def forward(self, x: torch.Tensor):
bsz, seqlen, _ = x.shape
xq, xk, xv = self.wq(x), self.wk(x), self.wv(x)
xq = xq.view(bsz, seqlen, self.n_local_heads, self.head_dim)
xk = xk.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)
xv = xv.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)
# attention 操作之前,应用旋转位置编码
xq, xk = apply_rotary_emb(xq, xk, freqs_cis=freqs_cis)
#...
# 进行后续Attention计算
scores = torch.matmul(xq, xk.transpose(1, 2)) / math.sqrt(dim)
scores = F.softmax(scores.float(), dim=-1)
output = torch.matmul(scores, xv) # (batch_size, seq_len, dim)
# ......
3.3 - KV Cache
大模型推理性能优化的一个常用技术是KV Cache,那么什么是K V Cache呢?首先这里的K V 值得分别是Attention计算时的KV,而非哈希存储引擎中的Key和Value,这里的Cache也不是那个会发生Cache Missing的Cache , 这里的K V Cache就是将Attention 中的KV缓存下来,通过空间换时间的方式来加速计算Attention。
从第一节处理流程中我们可以知道,在LLama 2模型的推理阶段是采用自回归的方式来进行推理,即每一个Token的生成都是由之前所有生成的所有token作为输入而得到的。
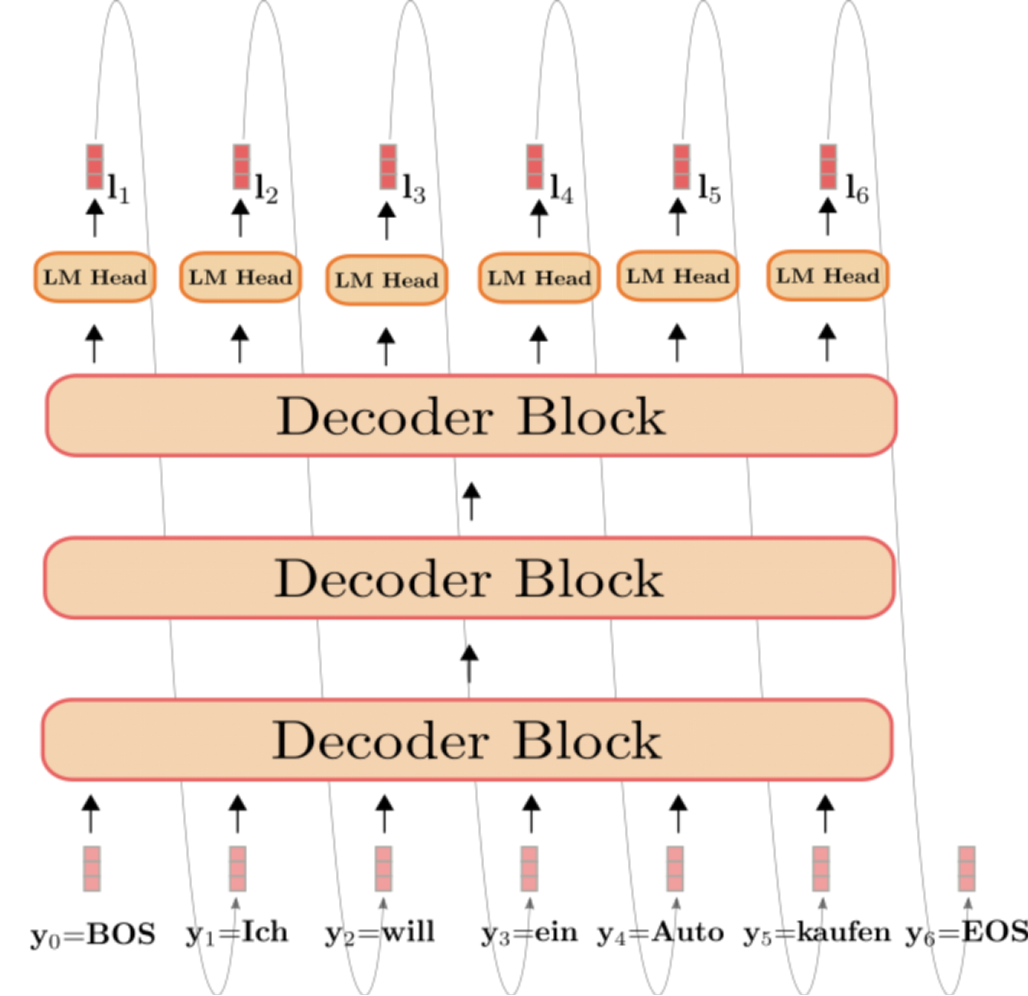
举个例子,假设有这样一个生成任务:
In [1]: {prompt:"将进酒:"}
Out [1]: 将进酒:人
In [2]: 将进酒:人
Out [2]: 将进酒:人生
In [3]: 将进酒:人生
Out [3]: 将进酒:人生得
In [4]: 将进酒:人生得
Out [4]: 将进酒:人生得意
In [5]: 将进酒:人生得意
Out [5]: 将进酒:人生得意需
In [6]: 将进酒:人生得意需
Out [6]: 将进酒:人生得意需尽
In [7]: 将进酒:人生得意需尽
Out [7]: 将进酒:人生得意需尽欢
而第四次的处理过程是用”将进酒:人生得” 来预测下一个”意”字,所以需要把”将进酒:人生得”进行token化后再进行Attention计算,即$Softmax(QK^T)V$,如下图所示:
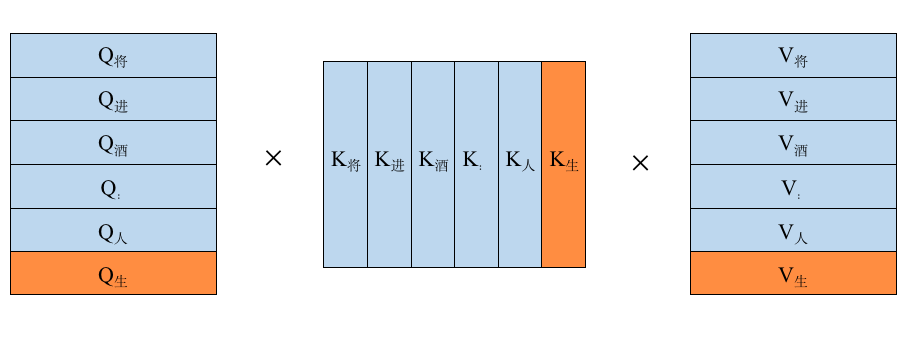
不难发现在第三次处理的时候,就已经把”将进酒:人生”所对应的Q,K,V进行过相关的运算,所以没必要在对他们进行Attention计算,这样就能节省大部分算力,由此K V Cache便是来解决这个问题的:通过将每次计算的K和V缓存下来,之后新的序列进来时只需要从KV Cache中读取之前的KV值即可,就不需要再去重复计算之前的KV了。此外,对于Q也不用将序列对应的所有$Q_i$都计算出来,只需要计算最新的$Q_{newtoken}$, (即此时句子长度为1), K V同理,所以我们用简易代码描述一下这个过程就是:
def mha(x, c_attn, c_proj, n_head, kvcache=None): # [n_seq, n_embd] -> [n_seq, n_embd]
# qkv projection
# when we pass kvcache, n_seq = 1. so we will compute new_q, new_k and new_v
x = linear(x, **c_attn) # [n_seq, n_embd] -> [n_seq, 3*n_embd]
# split into qkv
qkv = np.split(x, 3, axis=-1) # [n_seq, 3*n_embd] -> [3, n_seq, n_embd]
if kvcache:
# qkv
new_q, new_k, new_v = qkv # new_q, new_k, new_v = [1, n_embd]
old_k, old_v = kvcache
k = np.vstack([old_k, new_k]) # k = [n_seq, n_embd], where n_seq = prev_n_seq + 1
v = np.vstack([old_v, new_v]) # v = [n_seq, n_embd], where n_seq = prev_n_seq + 1
qkv = [new_q, k, v]
3.4 - Group Query Attention
但你转念一下,可是K,V 真的能缓存的了吗?我们来算笔账,以Llama 7B模型为例,hidden_size为4096,也就说每个K,V有4096 个数据,假设是半精度浮点数据float16,一个Transformer Block中就有 4096* 2 *2 = 16KB的单序列 K,V缓存空间,而Llama 2一共32个Transformer Block,所以单序列整个模型需要16 * 32 = 512KB的缓存空间,那多序列呢?如果此时句子长度为1024 ,那是不是就得512MB 的缓存空间了。而现在英伟达最好的卡 H100 的 SRAM 缓存大概是 50MB,而 A100 则是 40MB. 而 7B 模型都这样,175B 模型就更不用说了[5]。
既然SRAM 放不下,我们放到DRAM(GPU显存)行不行呢?答案是可以,但要牺牲性能。我们学过CUDA编程,我们知道全局内存(GPU)的读写速度要要远低于共享内存和寄存器,由此便会导致一个问题: Memory Wall(内存墙)。所谓内存墙简单点说就是你处理器ALU太快,但是你内存读写速度太慢跟不上,这就会导致ALU算晚之后在那等着你数据搬运过来,进而影响性能。
那么该如何解决呢?答案无非是从硬件层面和软件层面来说:从硬件层面,可以使用HBM(高速带宽内存)提高读取速度,或者抛弃冯诺依曼架构,改变计算单元从内存读数据的方式,不再以计算单元为中心,而以存储为中心,做成计算和存储一体的“存内计算”[5],比如”忆阻器”。而从软件层面就是优化算法,由此便引入Llama 2所使用的GQA (Group Query Attention)。
为了简单明了说明MQA GQA这里用GQA原论文的一个图来表示
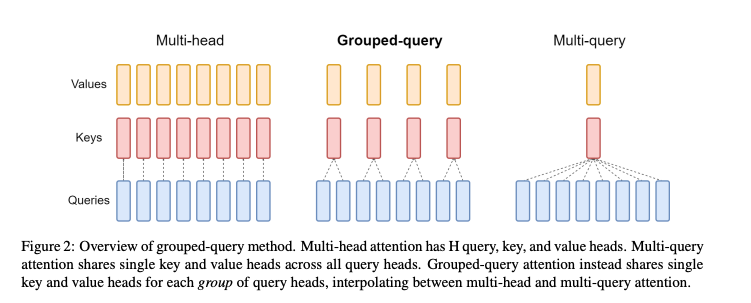
就如图例所言,多头注意力机制(MHA)就是多个头各自拥有自己的Q,K,V来算各自的Self-Attention,而MQA(Multi Query Attention)就是Q依然保持多头,但是K,V只有一个,所有多头的Q共享一个K,V ,这样做虽然能最大程度减少KV Cache所需的缓存空间,但是可想而知参数的减少意味着精度的下降,所以为了在精度和计算之间做一个trade-off,GQA (Group Query Attention)孕育而生,即Q依然是多头,但是分组共享K,V,即减少了K,V缓存所需的缓存空间,也暴露了大部分参数不至于精度损失严重。
3.5 - FeedForward
与标准的Transformer一样,经过Attention层之后就进行FeedForward层的处理,但LLama2的FeedForward与标准的Transformer FeedForward有一些细微的差异,这块没啥好讲的,看代码就行,需要注意的地方就是SiLU激活函数
\[SiLU(x)=x*Sigmoid(x)=\frac{x}{1+e^{-x}}\]class FeedForward(nn.Module):
def __init__(
self,
dim: int,
hidden_dim: int,
multiple_of: int,
ffn_dim_multiplier: Optional[float],
):
super().__init__()
hidden_dim = int(2 * hidden_dim / 3)
# custom dim factor multiplier
if ffn_dim_multiplier is not None:
hidden_dim = int(ffn_dim_multiplier * hidden_dim)
hidden_dim = multiple_of * ((hidden_dim + multiple_of - 1) // multiple_of)
# Linear 1
self.w1 = ColumnParallelLinear(...)
# Linear 2
self.w2 = RowParallelLinear(...)
# Linear 3
self.w3 = ColumnParallelLinear(...)
def forward(self, x):
return self.w2(F.silu(self.w1(x)) * self.w3(x))
4 - Training
超参数:
- AdamW 优化器,β1 = 0.9, β2 = 0.95, eps = 10.5
- cosine 学习率调度,warmup of 2000 steps ,最终学习率衰减到最大值的10%
- 权重衰减(weight decay) 0.1
- 梯度裁剪(gradient clipping) 1.0
分词器(Tokenizer)
- BPE,使用 SentencePiece 实现
- 所有数字 split 成 individual digits
- 未知的 UTF-8 字符用 byte 表示
- 词表大小 32K
训练效果:
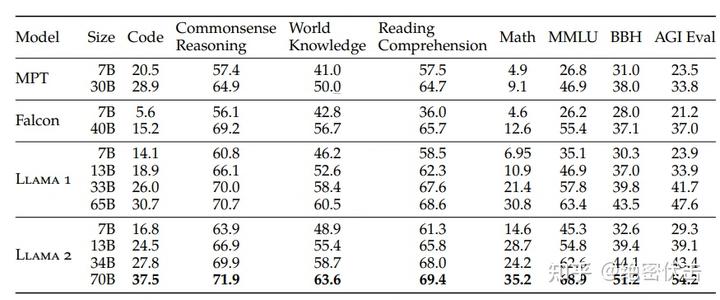
5 - 推理与部署优化
推理性能常受显存带宽与注意力计算限制。实践中常结合 FlashAttention/Flash‑Decoding、Paged‑KV(分页式 KV 管理)、多流并发与批内/批间重用提升吞吐;在模型侧配合量化(INT8/INT4、AWQ、GPTQ/FP8 等)降低显存占用,并通过分块推理削峰。多卡部署时可引入张量/流水并行与高带宽互联(NVLink/NVSwitch)稳定大批量吞吐。
6 - 对齐与微调
Llama 2 的对齐通常采用“预训练 + 指令监督微调(SFT)+ 反馈优化(RLHF/RLAIF)”范式。SFT 保证遵循指令与格式,RLHF 通过偏好优化在安全性、礼貌性与有用性上做约束。行业落地常用 LoRA/QLoRA 做高效参数微调,并结合检索增强(RAG)保证知识新鲜度。
7 - 小结
Llama 2 以 RMSNorm、RoPE、GQA、SwiGLU 与高效推理技术构成“性能‑成本‑易用性”的平衡。理解其架构与工程优化,有助于在有限资源下获得稳定的任务效果。
