Batch Normalization(以下用 BN 简称)旨在缓解深度网络中的“Internal Covariate Shift(内部协变量移位)”,对同一 mini‑batch 的特征做标准化,使得训练可使用更大的学习率并加快收敛,同时降低对初始化的敏感性。所谓内部协变量移位,是指随着层数加深、参数更新导致每层输入分布不断变化,进而增加优化难度。
Introduce BN
BN 的直觉接近“白化”:将每一层的输入标准化为零均值、单位方差,从而缓解梯度消失并支持更大的学习率。
一般会有以下两种对不同阶段BN的操作方法:
- 在forward process前向传递过程中进行BN,而在backward process后向传递的过程中无视其他样本对当前样本的影响。举个例子,对于某一层的输入$\mu$和学习到的偏移量$b$,进行白化$\hat{x}=x-E[x]$,其中$x=\mu+b$,进行梯度更新时$b=b+\Delta b$,$\Delta b=-\frac{\partial l}{\partial b}$,而输出$\hat{x}’=\mu+(b+\Delta b)-E[\mu+(b+\Delta b)]=\mu+b-E[\mu+b]$,可以看出该层的输出和损失没有任何变化,但随着更新$b$会趋近于无穷。所以在normalization时要考虑优化的过程。
- 在前向传播进行normalization,反向传播考虑其他样本数据对于当前样本的影响。如果将normalization过程看做一次变化,$\hat{x}=Norm(x, \chi)$。反向传播时考虑其他样本数据对当前样本的影响,需要计算两个导数:$\frac{\partial Norm(x, \chi)}{\partial x}$和$\frac{\partial Norm(x, \chi)}{\partial \chi}$,其中第二个计算的复杂度较大。
为此有两处做了简化:
-
对每个特征独立的进行normalization。
-
简单的normalization每一层的输入降低了模型的表现能力,比如norm后通过sigmoid激活函数数据分布在中间线性的区域,所以加入可学习的参数进行scale and shift。
Method
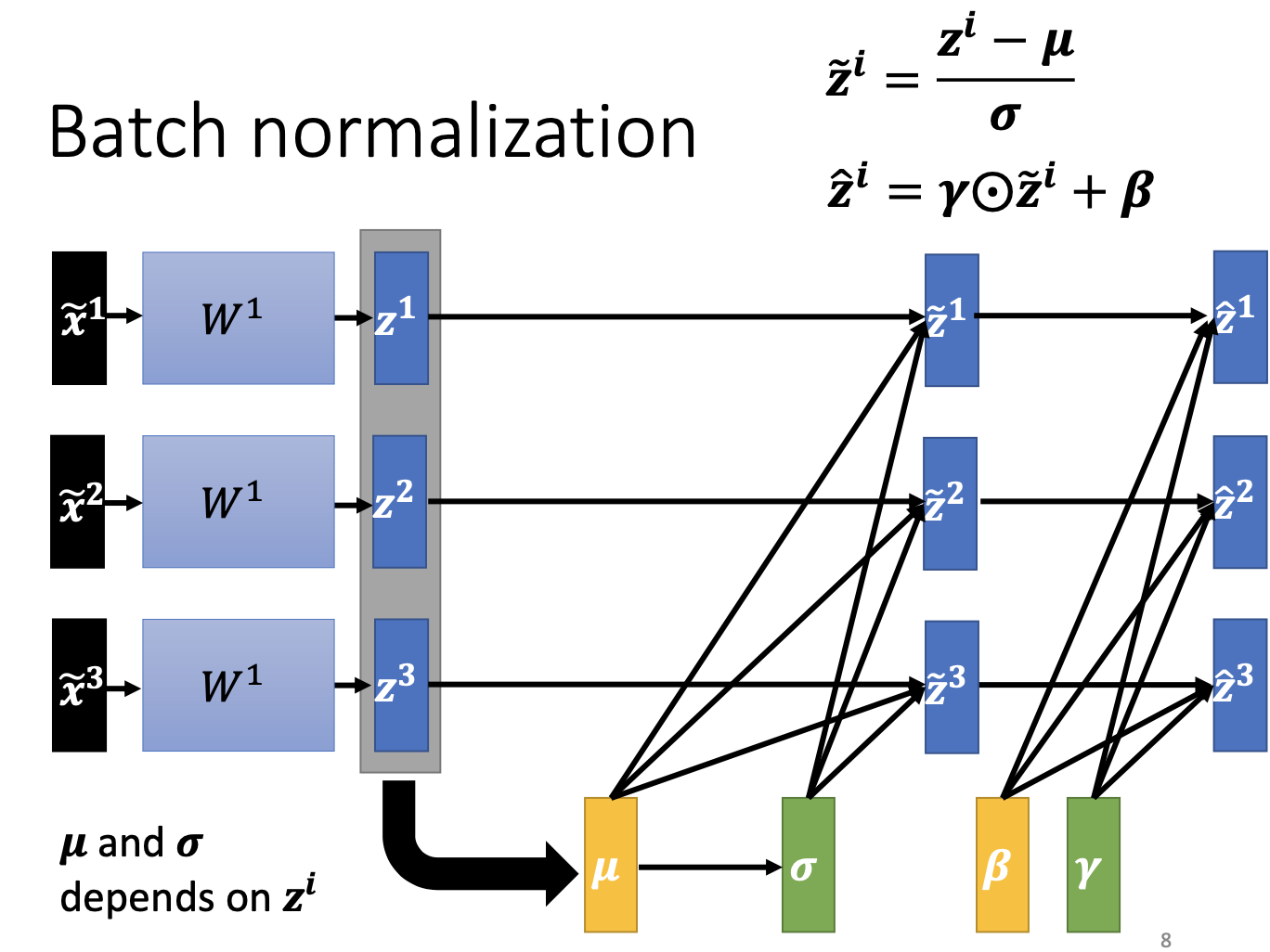
如果 batch size 为 m,则在前向时每个节点都有 m 个输出,对该 m 个值做标准化。两步:
- Standardization:对 m 个 $x$ 标准化得到 $\hat{x}$;
- Scale and shift:对 $\hat{x}$ 进行缩放和平移,得到最终输出 $y$。其中 $\gamma$ 与 $\beta$ 为可学习参数。

针对 Batch Normalization Transform,总体可写为:
$\mathrm{BN}(x_i^{(b)})= \gamma\cdot\frac{x_i^{(b)}-\mu_\beta}{\sqrt{\sigma_\beta^2+\epsilon}}+\beta$
整体变化流程如下图所示:
Forward/Backward 公式
设某一层单通道在一个 mini‑batch 上有 m 个样本(卷积层中按 N×H×W 展平计数):
- 均值:(\mu_\beta=\tfrac{1}{m}\sum_i x_i)
- 方差:(\sigma_\beta^2=\tfrac{1}{m}\sum_i (x_i-\mu_\beta)^2)
- 标准化:(\hat{x}i=\tfrac{x_i-\mu\beta}{\sqrt{\sigma_\beta^2+\epsilon}})
- 仿射:(y_i=\gamma\hat{x}_i+\beta)
反向传播(给定上游梯度 (g_i=\partial\mathcal{L}/\partial y_i)):
- (\partial\mathcal{L}/\partial\beta=\sum_i g_i)
- (\partial\mathcal{L}/\partial\gamma=\sum_i g_i\,\hat{x}_i)
- (\partial\mathcal{L}/\partial x_i=\frac{\gamma}{m\sqrt{\sigma_\beta^2+\epsilon}}\left[m\,g_i-\sum_j g_j-\hat{x}_i\sum_j (g_j\,\hat{x}_j)\right])
该式展示了“批间耦合”的来源:每个样本的梯度依赖于同批次其他样本的 (g_j)。
Training & Testing
训练阶段,$\mu,\sigma$ 取自当前 mini‑batch 的统计量;推理阶段应固定为“人口统计量”(running mean/var),通常用指数滑动平均(EMA)在训练中累积得到。

实现细节(Conv 层):对每个通道独立归一化,均值/方差在 N×H×W 维度上统计;(\gamma,\beta) 的形状为 C。常见的 BN1d/BN2d/BN3d 仅对应不同的统计维度约定。
Effect
- 可以使用更大的学习率,训练更稳定、收敛更快。
- 可以将bias置为0,因为Batch Normalization的Standardization过程会移除直流分量,所以不再需要bias。
- 对权重初始化不再敏感,通常权重采样自0均值某方差的高斯分布,以往对高斯分布的方差设置十分重要,有了Batch Normalization后,对与同一个输出节点相连的权重进行放缩,其标准差σσ也会放缩同样的倍数,相除抵消。
- 对权重的尺度不再敏感,理由同上,尺度统一由$\gamma$参数控制,在训练中决定。
- 深层网络可以使用sigmoid和tanh了,理由同上,BN抑制了梯度消失。
- 具备一定正则作用,可适度降低对 dropout 的依赖。
- 加速学习率衰减,因为可以比inception更快训练,所以可以将学习率衰减速率增加到其6倍。
- 可替代 LRN(Local Response Norm),后者稳定性较差。
- 更彻底地shuffle训练样本,BN更受益于样本内部更大的随机性。
- 减少光度畸变(photometric distortions)敏感性,更关注有效样本而非强增广噪声。
实践要点
- 层内顺序:常用
Conv → BN → ReLU;在 Pre‑Activation ResNet 中用BN → ReLU → Conv。 - 超参:
momentum控制 EMA 更新速率(常 0.9/0.99),eps防止除零(1e‑5/1e‑3)。 - 小 batch:当每卡样本数过小,mini‑batch 统计量噪声大,建议使用 SyncBN、FreezeBN/PreciseBN 或改用 GN。
- 梯度累积不等于大 batch 统计:累积只影响优化步长,不会改变 BN 的统计量维度。
常见易错点与排坑:
- 冻结 BN(FrozenBN):微调小数据集或检测/分割下游任务时,常固定 running mean/var 与 (\gamma,\beta)(或仅固定统计量),防止统计漂移;
- 混合精度:保持 BN 统计在 FP32 进行更稳的均值/方差计算;
- 分布式:若使用 SyncBN,确认通信分组与 world size;对超大分辨率可分层同步(仅主干同步,head 层使用本地 BN)。
统计与泛化
在实际训练中,BN 的统计量如何获得、如何在不同 batch 尺度与不同数据分布下保持稳定,直接决定了模型的可泛化性。
首先,运行时均值与方差若仅由 EMA 累积,可能出现收敛偏差。为此,可在同一权重下用若干 mini‑batches 专门收集统计量,并聚合成更接近总体的估计(俗称 PreciseBN):
$\mu_{pop}=\mathbb{E}[\mu_\beta],\quad \sigma^2{pop}=\mathbb{E}[\mu\beta^2+\sigma_\beta^2]-\mathbb{E}[\mu_\beta]^2$。
其次,需区分两种 batch 尺度:用于优化的全局 SGD batch size,以及参与统计的 Normalization batch size(单卡或同步后)。后者过小会带来更大的训练噪声与 train‑test 不一致;经验上 32–128 的归一化批量更稳。工程上常见做法是在训练后期切换到 Frozen/PreciseBN,以稳定 population 统计进行推理;个别线上场景也会在推理阶段沿用 mini‑batch 统计,但需评估延迟与可重复性。
当训练域与推理域存在差异(domain shift)时,建议使用评估域上收集到的 population 统计量;若多域联合训练,尽量保持“优化、统计收集、评估”三者的域一致,或采用 domain‑specific 统计以降低偏移。
最后,BN 的“批内共享统计”带来一种信息泄漏:同一 mini‑batch 内样本在标准化时彼此可见。对于检测/分割等多目标任务,可通过 SyncBN、跨 GPU 打散 RoI features、或在 head 前随机重分配样本来减弱相关性;在超大分辨率下,也可仅对主干启用同步,而在 head 使用本地 BN,以在稳定与开销之间取得平衡。
Group Normalization(GN)
BN 依赖 batch 统计,在小 batch 或多域场景表现欠佳。Group Normalization 按通道分组做标准化:将特征从 [N,C,H,W] reshape 为 [N,G,C//G,H,W],在每组上计算均值/方差并归一化,最后再使用可学习的 $\gamma,\beta$ 做仿射变换。极端情形下:G=C 退化为 LayerNorm,G=1 退化为 InstanceNorm。经验上 G=32 常见。
优点:对 batch size 鲁棒;在检测/分割/视频等任务中稳定。缺点:在大 batch 分类上有时略逊于 BN。
何时使用 BN / GN / LN / IN
- 大 batch、单域训练:优先 BN(含 SyncBN)。
- 小 batch、多卡微批:GN 或 Frozen/PreciseBN;检测/分割常选 GN。
- 语言/自回归等序列模型:LN 常用。
- 风格迁移/生成:IN 常见。
Summary
- 卷积层如何使用Batch Norm?
1个卷积核产生1个feature map,1个feature map有1对$\gamma$和$\beta$参数,同一batch同channel的feature map共享同一对$\gamma$和$\beta$参数,若卷积层有n个卷积核,则有n对$\gamma$和$\beta$参数。
- 没有scale and shift过程可不可以?
可以,但网络的表达能力会下降。对输入进行scale and shift,有利于分布与权重的相互协调。
- BN层放在ReLU前面还是后面?
原paper建议将BN层放置在ReLU前,因为ReLU激活函数的输出非负,不能近似为高斯分布。实验表明,放在前后的差异似乎不大,甚至放在ReLU后还好一些。
-
BN层为什么有效?
- BN层让损失函数更平滑:加BN层后,损失函数的landscape(loss surface)变得更平滑,相比高低不平上下起伏的loss surface,平滑loss surface的梯度预测性更好,可以选取较大的步长。
- BN更有利于梯度下降:没有BN层的,其loss surface存在较大的高原,有BN层的则没有高原,而是山峰,因此更容易下降。
- 没有BN层的情况下,网络没办法直接控制每层输入的分布,其分布前面层的权重共同决定,或者说分布的均值和方差“隐藏”在前面层的每个权重中,网络若想调整其分布,需要通过复杂的反向传播过程调整前面的每个权重实现,BN层的存在相当于将分布的均值和方差从权重中剥离了出来,只需调整$\gamma$和$\beta$两个参数就可以直接调整分布,让分布和权重的配合变得更加容易。
