推测解码(Speculative Decoding)是一种大模型的推理加速方式。
传统的解码方式需要逐步调用大模型自回归地预测每个单词,耗时较长。推测解码使用某种方法,先生成一系列草稿 tokens,将这些草稿作为候选序列传入大模型,然后由大模型在单次前向传播中验证这些候选序列是否符合其高质量生成标准。因此,推测解码分为 “草稿 draft” 和 “验证 verify” 两个串行阶段。
这使得大模型避免了逐个 token 推理的过程,大幅减少计算时间,同时保留了生成的连贯性和准确性。如果利用得当,推测解码可以在不牺牲大模型生成质量的情况下,大幅增加大模型的解码速度。
分类
目前的推测解码(Speculative Decoding)方法可以大致分为 3 类:
- 在内存中同时加载一个小草稿模型,辅助生成草稿(最初的 Speculative Decoding 论文提出的方法)。这个小草稿模型可以是同系列的参数更小的模型,也可能是额外训练的轻量级模块;
- 直接将大模型同时作为起草模型和验证模型。这种方法往往会对原始模型结构做一些修改,或使用额外数据再微调大模型;
- 从外部数据中(如外部数据库或 prompt)检索获取草稿来源。
术语与评价指标
在工程实践中,我们通常用几类量来刻画推测解码是否“又快又稳”。接受率(Acceptance)衡量被大模型验证通过的草稿比例,它直接决定加速的上限;草稿的深度与宽度反映一次起草的长度和分支数,深且宽往往提升接受率,但也会推高显存开销;验证成本(Verify cost)对应大模型单次前向的算力与带宽消耗,若采用树状验证,成本可以在多个候选之间摊薄。最后,评估应同时给出端到端吞吐与时延(如 tok/s、P50/P95)以及质量指标(BLEU、BERTScore 或人评),避免只看速度而忽略输出质量。
Acceptance 规则与一致性
不同方法对“验证是否通过”的定义并不相同。严格的一致性要求候选与大模型在目标策略下的选择完全一致(例如贪婪路径或与温度采样等价的随机过程),优点是分布无偏,缺点是接受率通常较低。相对宽松的“典型接受”会在给定阈值内接纳高概率候选,显著提高接受率,但需要额外监控质量漂移并在高风险场景(如代码、医疗)回退到严格规则。对于温度、Top‑k 或核采样(Top‑p)等非贪婪策略,还应明确接受规则与采样过程的一致性,以免引入统计偏移。
工程化实践与建议
要把速度优势转化为稳定的线上收益,核心在于数据与算力的管线化。首先复用并精确管理 KV Cache,在树状验证时用“只看祖先”的掩码确保语义正确;其次通过长度分桶、动态 padding 或连续批处理缓解批内对齐问题,并关注验证分支的内核效率。起草模型可以是小模型、特征外推器(如 EAGLE)或层跳跃版本,选型应比较“接受率 × 起草速度 × 验证成本”的乘积而非单点指标。最后,配套一套可观测性面板,持续跟踪接受率分布、草稿深度、验证利用率以及端到端吞吐/时延与质量,便于快速定位瓶颈。
小模型draft+大模型verify
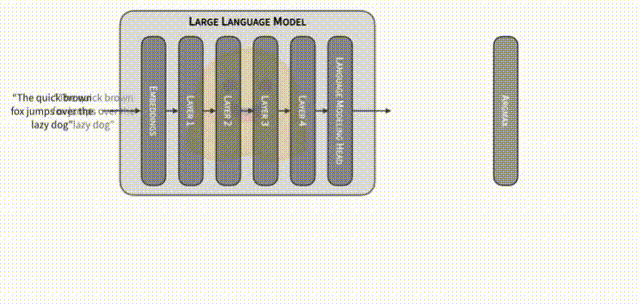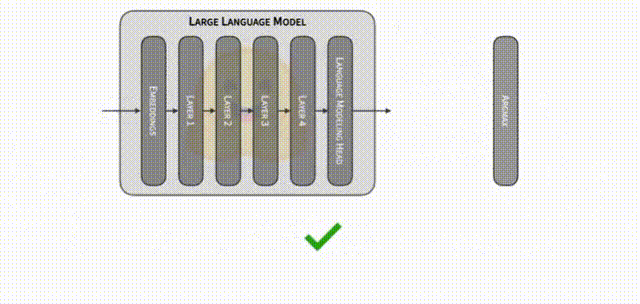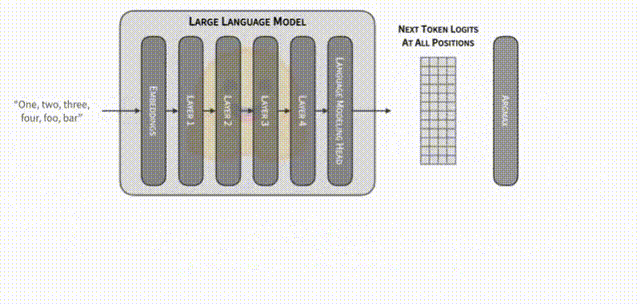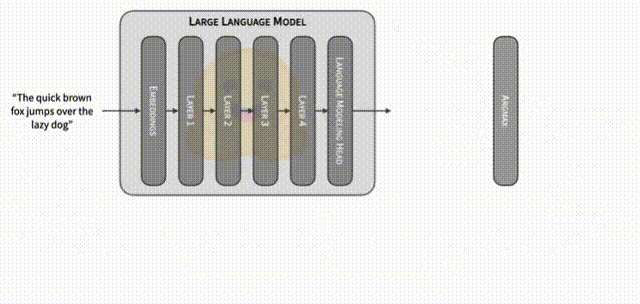
推测解码的核心思想在于充分利用大模型的 logits 层输出信息,而不仅仅是最后一个输出的 logits 向量的信息,在单次前向传播中实现对多个候选后续序列的验证。
其基本方法是:
- Drafting/草稿阶段:使用某种方法(小草稿模型或大模型本身),对下一个可能出现的一批 token 进行预生成。也就是说,在大模型自回归生成一个 token 之前,先行快速给出一批候选 token 序列。
- Validation/验证阶段:将这批候选 token 序列连同原有上下文输入大模型,通过禁用缓存或重新传入完整序列等方式,使大模型在一次前向计算中输出相应位置上的 logits 分布。在这里,大模型能通过单次前向传播就给出整个草稿序列的各位置下一步 token 的概率向量。通过将大模型针对这些位置所得的概率分布与草稿序列进行对比,可以快速判断每个草稿 token 是否与大模型的真实预测概率匹配。
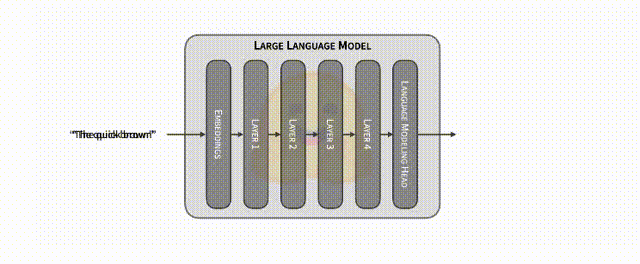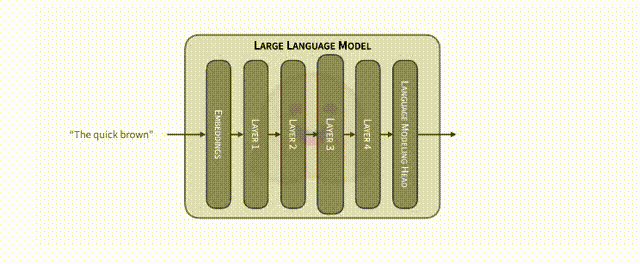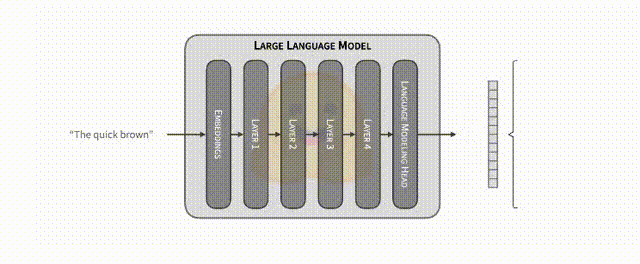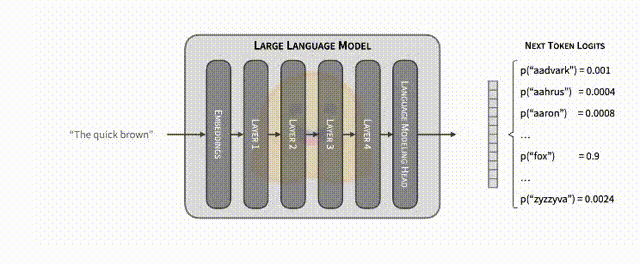
- 筛选和确认:若猜测的 token 序列在大模型的 logits 确认下可信(即与大模型可能选择的高概率 token 一致),则直接接受整个草稿序列,从而节省了逐 token 生成的反复计算时间;若猜测不符,则丢弃并重新尝试。
在贪婪解码情境下,推测解码之所以能够在理论上保留与大模型原本逐步生成相同的概率分布特征,其关键在于“确认”步骤的严格性。贪婪解码策略下,大模型在每个位置都会选择当前概率分布中最高概率的下一个 token。推测解码既没有改变大模型给出概率分布的方式,也没有在最终决策上偏离大模型的“贪婪”选择逻辑。它只是在过程中预先尝试一批潜在的后续 token,并使用大模型原本的概率分布为标准进行严格筛选。一旦筛选通过,就说明这些 token 本来就是大模型在逐 token 解码中所可能给出的最高概率路径,从而保证最终输出与传统自回归解码的结果在理论上是一致的。这一过程并未更改大模型本来的输出分布,只是通过“提前拟合 + 后验验证”的方式,加快了确认下一个最优 token 的决策速度。
Eagle
Eagle 是 Google 的一个开源项目,它利用了 Speculative Decoding 的思想,实现了一种基于大模型 Drafting 的方法,以加速大模型的解码速度。它的创新点在于,不直接对下一步 token 进行预测,而是对原始大模型内部的最后一个隐藏层特征(来自 lm_head 前面一层的 feature)进行外推(extrapolate)。
EAGLE 引入了一个轻量级的自回归头(Auto-regression Head),基于当前特征序列预测下一个特征,最后通过冻结的分类头将 features 映射为 tokens。这种方法的优势在于,features 比 tokens 更具结构性和规律性,因此能达到更好的草稿接受率。此外,EAGLE在起草阶段采用树状生成结构,使得在验证阶段可以通过一次前向传播处理多个 tokens,从而提高了解码效率。
- EAGLE 与 SpecInfer 和 Medusa 类似,采用树注意力机制,草稿的生成和验证都是树结构的。
- 需要一个基础大模型和一个附加模块(FeatExtrapolator),这个 FeatExtrapolator模块的参数量远小于大模型,例如70B的大模型对应1B的 FeatExtrapolator。

与其他方法只基于 token 进行起草不同,EAGLE 还基于 feature 序列(f4, f5)进行起草。
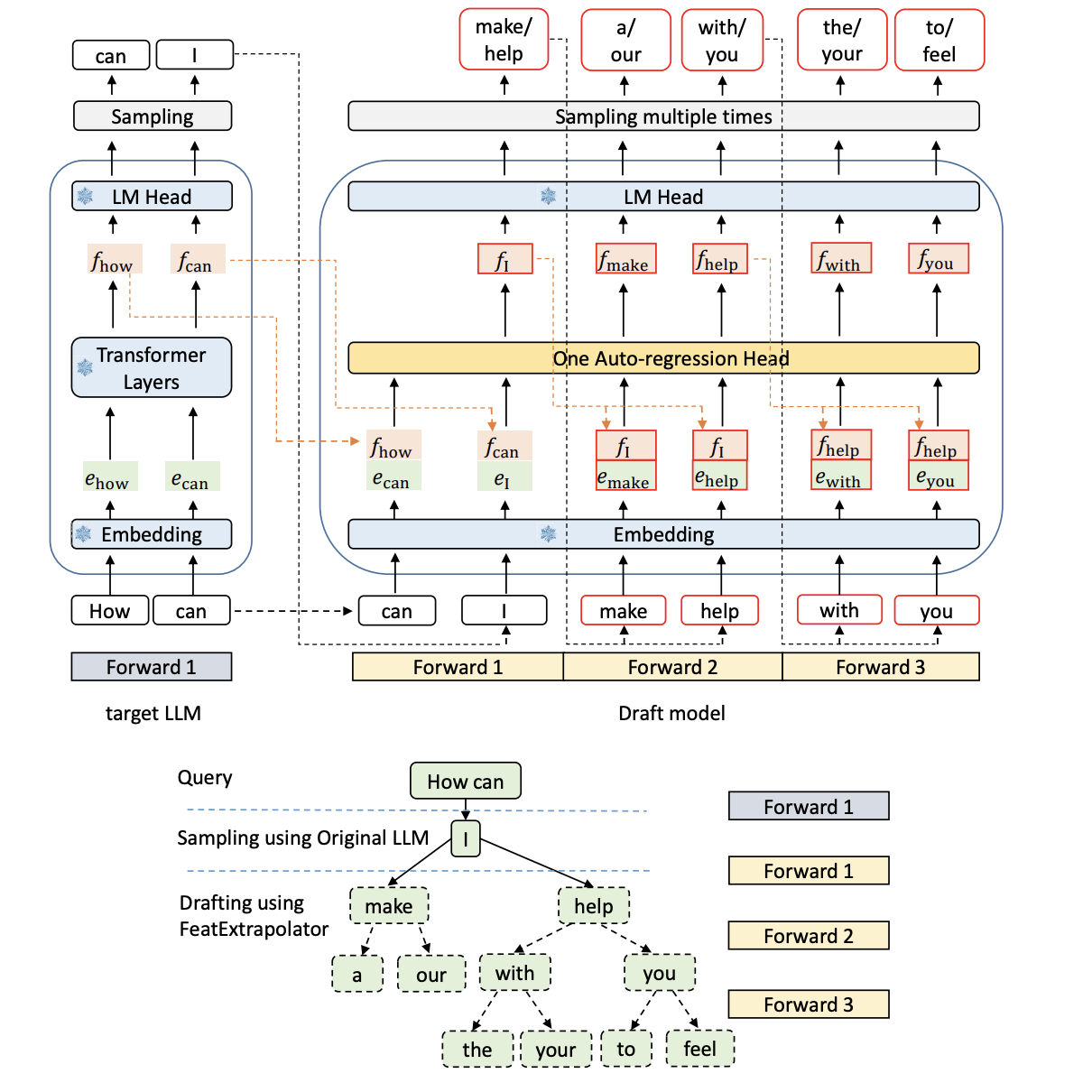
具体流程如下:
- 初始前向计算(原模型生成初始特征和下一个token): 首先使用原始LLM对给定的输入prompt进行一次标准的自回归前向传播,得到下一 token 的特征表示(第二高层特征)和对应的token输出。这一步是正常解码的开始点,得到初始的已知特征和token。
- 特征外推(起草): 利用上述已获得的特征和当前 token 的词嵌入,输入到轻量的 Auto-regression Head(FeatExtrapolator)中进行预测。该头通过自回归方式生成后续的特征序列(即对下一步、下下步的特征进行外推预测)。 在得到这些预测特征后,使用冻结的LM头将这些特征映射回 token 分布,并根据该分布进行采样,得到多条可能的token序列分支。最后在特征层面快速生成了一个树形的候选token集。
- 多轮推测与树状生成: 重复上述特征外推和token生成的过程多次,即在每一轮中,从当前已验证的token和特征出发,通过 FeatExtrapolator 再猜测多个后续特征点,并通过 LM头生成多个候选 token 分支,形成一颗较为稀疏的预测树。这一过程仅使用小模型(FeatExtrapolator)快速起草出大量候选序列。
- 验证(单次前向评估原LLM): 对通过树状起草的候选序列进行验证,即使用原始LLM进行一次前向传播,验证这些猜测路径中哪些分支的token是与原LLM分布一致的,并选出要接受的token。
Eagle-2
相比EAGLE-1的改进:
- 在 EAGLE-1 中使用静态 draft 树,这假设 draft tokens 的接受率仅取决于它们的位置。但是现在,我们发现 draft tokens 的接受率还取决于上下文。因此 EAGLE-2 使用了一种具有上下文感知的动态draft树。
- 回归了传统推测采样(speculative sampling)方法的假设:根据上下文的变化,某些 tokens 更简单,更容易通过较小的草稿模型预测。
EAGLE-2 在 EAGLE 的基础上,通过 扩展(Expand)和 重排序(Rerank)两个阶段实现对 draft 树的动态调整,实现了对生成过程的进一步优化和加速,提高了对高价值分支的优先性,从而在验证前就大幅减少了需要处理的冗余候选序列。
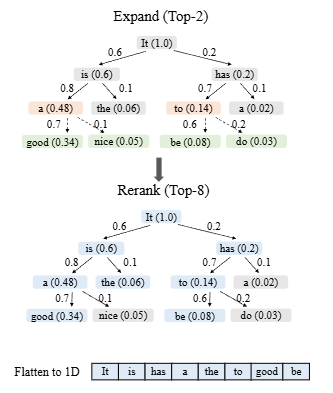
- 扩展阶段(Expansion Phase):
- 在当前层中,根据全局接受率(通过节点接受率与置信度近似计算得到的值)对节点进行排名。
- 选取 top-k 个具有最高全局接受概率的节点作为输入,再次输入给起草模型进行下一层候选 token 的生成,从而扩展起草树。这样就避免了过度扩张,减少了单次前向计算的负担。
- 重排序阶段(Reranking Phase):
- 在扩张完成后,对所有已生成的候选 token 节点(包括浅层和深层)进行全局排序,选取 top-m 个最有可能被接受的 token。
- 对于同值节点优先选浅层节点,以确保选出的前 m 个 token 仍然保持一个树状结构。
- 将这些选中的节点线性化成一条序列,以作为下一步验证阶段的输入。
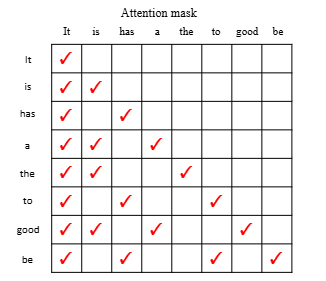
Attention Mask 的调整。因为最终输入给 LLM 验证的序列来自一棵树的不同分支,这些分支不应共享上下文。通过调整注意力掩码,只让每个 token 看见它的祖先节点,保证生成和原始自回归过程在信息可见性上的一致性。
大模型draft+verify
Medusa
Medusa 是一种不需要小草稿模型,而是通过扩展大模型结构本身来实现推测解码的方法。它在大模型中添加多个额外的并行解码头 “Medusa heads”,这些解码头与原始模型无缝集成,并且使用 tree-based attention 并行验证多个候选序列。Medusa Heads 需要经过微调,主干网络会被冻结。
Medusa Heads
每个 Medusa Head 实现为单层前馈网络,并通过残差连接进行对齐。每个 Medusa Head 位于大模型的 lm_head 之前,接受 last hidden state 作为输入,输出预测的单个 token。在单次前向传播中,第一个 Medusa Head 预测输入序列的下一个(第i+1)token,第二个 Medusa Head 预测输入序列的偏移量为(i+2)个 token。
self.medusa_head = nn.ModuleList([
nn.Sequential(
*([ResBlock(self.hidden_size)] * medusa_num_layers),
nn.Linear(self.hidden_size, self.vocab_size, bias=False),
)
for _ in range(medusa_num_heads)
])
Tree-based Attention
Medusa 使用 tree-based attention 并行验证多个候选序列。在每个 Medusa Head 中,使用 tree-based attention 来计算每个候选序列的 logits。Medusa 采用自上而下的方法构建树,对于每个 Medusa Head 生成的候选 token 作笛卡尔积(Cartesian product):
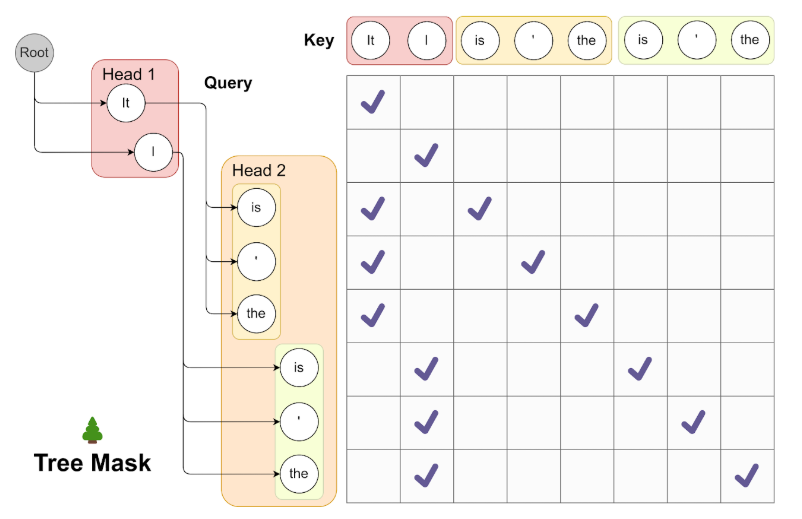
在上图中,第一个 Medusa Head 的前 2 个预测 token (It, I) 和第二个 Medusa Head 的前 3 个预测 token (is, ’, the) 总共产生 2 × 3 = 6 个 candidates(候选序列),这些 candidates 中的每一个都对应树中的一个不同分支。
为了保证每个 Token 只访问其前驱,本文重新设计了 attention mask,它只允许 Attention 从当前 Token 流回其前驱 Token。位置编码的位置索引(position idx)会根据此结构进行调整。
Sparse Tree
当每个 Medusa Head 取 top-k个(而不是top-1)草稿 token 时,树的路径数就会急剧增多,因此设计了一种稀疏化注意力树的方法。在实验中,具有 64 个节点的稀疏树比具有 256 个节点的密集树显示出更好的加速比。
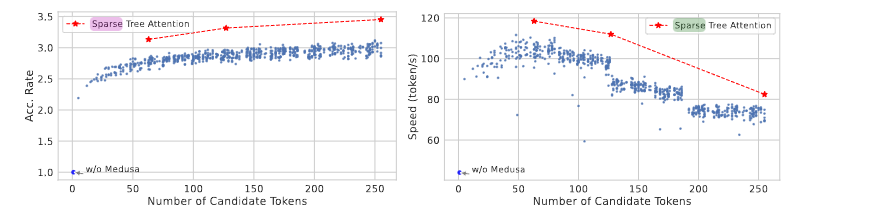
Implementation
首先调用 [utils.py] 的 generate_medusa_buffers 函数,得到一个初始化的稀疏树结构,这个函数为每条路径创建一个祖先节点索引列表,以便在后续进行验证时能够快速找到与当前节点路径相关的所有祖先路径:
retrieve_indices_nest = []
retrieve_paths = []
for i in range(len(sorted_medusa_choices)):
cur_medusa_choice = sorted_medusa_choices[-i-1] # 从列表末尾开始处理路径
retrieve_indice = []
if cur_medusa_choice in retrieve_paths:
continue
else:
for c in range(len(cur_medusa_choice)):
# 对于当前路径的每个前缀子路径(从 root 一直到当前深度的子路径),
# 找出其在 sorted_medusa_choices 中的索引。
subpath = cur_medusa_choice[:c+1]
retrieve_indice.append(sorted_medusa_choices.index(subpath))
retrieve_paths.append(subpath)
retrieve_indices_nest.append(retrieve_indice)
- 逆序处理路径:cur_medusa_choice = sorted_medusa_choices[-i-1] 从列表的末尾往前取路径,保证了当处理深层节点时,其祖先路径也已处理过。
- if cur_medusa_choice in retrieve_paths: continue 用于对路径去重,避免重复处理相同路径。
- 构造单条路径的祖先索引列表:对 cur_medusa_choice 的每个前缀 cur_medusa_choice[:c+1],找到该前缀路径在 sorted_medusa_choices 中的全局索引并加入 retrieve_indice。这样 retrieve_indice 就变成从根节点开始,一直到当前路径末尾的一个祖先链条的全局索引序列。
完成后 retrieve_indices_nest 是一个嵌套列表,每个子列表代表一条路径及其所有祖先路径在 sorted_medusa_choices 中的索引序列:
max_length = max([len(x) for x in retrieve_indices_nest])
retrieve_indices = [pad_path(path, max_length) for path in retrieve_indices_nest]
retrieve_indices = torch.tensor(retrieve_indices, dtype=torch.long)
retrieve_indices = retrieve_indices + 1
retrieve_indices = torch.cat([torch.zeros((retrieve_indices.shape[0], 1), dtype=torch.long), retrieve_indices], dim=1)
最终将生成的所有张量聚合到一个字典 medusa_buffers 中,返回这个 medusa_buffers。
然后回到 [medusa_model_new.py],将 medusa_buffers 传入 generate_candidates 函数生成候选 candidates 序列,
for idx in range(max_steps):
# Generate candidates with topk predictions from Medusa heads
candidates, tree_candidates = generate_candidates(
medusa_logits,
logits,
medusa_buffers["tree_indices"],
medusa_buffers["retrieve_indices"],
…
)
得到候选序列后,再对其应用 tree_decoding 函数,tree_decoding 大致具有三个步骤:
- 通过将 Medusa position IDs 添加到输入序列,计算新的位置 ID。
- 使用大模型来 decode the tree candidates,模型返回原始 logit 和可能的其他输出的 logit。
- 根据 retrieve_indices重新排序获得的 logit,以确保与 reference 顺序一致。
# Use tree attention to verify the candidates and get predictions
medusa_logits, logits, outputs = tree_decoding(
tree_candidates,
past_key_values,
medusa_buffers["medusa_position_ids"],
medusa_buffers["retrieve_indices"],
)
小结
Medusa 真正吸引人的地方在于它上一步生成草稿,后续就可以直接把生成的草稿送进 lm_head 验证,在单次前向传播中同时做到草稿+验证,这一点看起来比 Draft & Verify 好,也避免了生成草稿阶段的推理延迟和显存占用问题。
文章更集中于测试其在放宽验证标准下(Typical Acceptance)的结果,这部分的结果无法保证模型的生成质量;
我们确定通常没有必要匹配原始模型的分布。因此,我们建议采用 Typical Acceptance 方案来选择合理的candidates
在贪婪解码下,虽然接受率很低(约 0.6),但从文章的测试结果来看,整体加速比也能达到不错的效果,这可能主要来源于整体“草稿 + 验证”流水的提速。
Hydra
Hydra 是对Medusa 的改进,它对 Medusa Heads 的结构进行了简单的更改。在 Medusa 中,所有Medusa Heads都是独立的,但 Hydra Heads 会将 candidate 序列中的早期 tokens 作为附加输入:
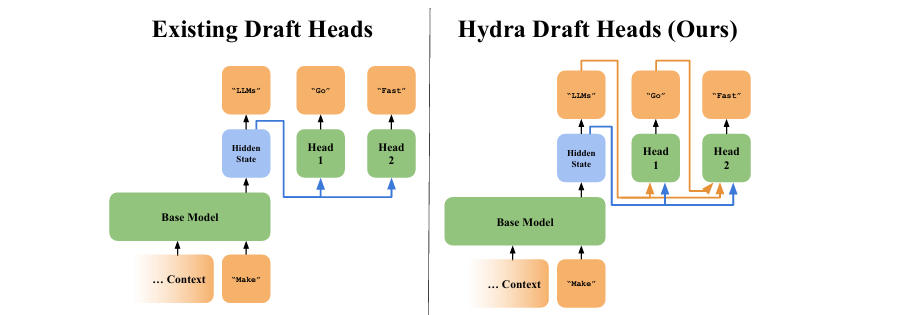
Hydra 头是顺序依赖的,因为它们是位于时间步 t 的基础模型的hidden states(hydra_hidden_states)与先前 Hydra 头生成的 tokens 的 input embeddings 的函数(the input embeddings of the tokens sampled by previous Hydra heads)。
hydra_hidden_states = []
with torch.inference_mode():
input_embeds = self.input_embed_fn(input_ids)
hydra_inputs = [prefix_embedding]
for i in range(self.hydra_num_heads):
# 将input_embeds的向量沿第1维(时间步或序列维度)滚动-(i+1)个位置。每个Hydra头都会收到一个被移位的版本
hydra_inputs.append(torch.roll(input_embeds, shifts=-(i+1), dims=1))
for i in range(self.hydra_num_heads):
# 从hydra_inputs中取前i+2个输入,沿最后一个维度拼接
head_input = torch.cat(hydra_inputs[:i + 2], dim=-1)
hydra_hidden_states.append(self.hydra_mlp[i](head_input))
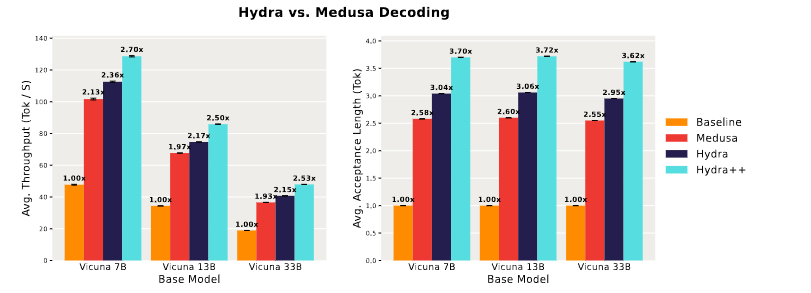
Hydra++
Hydra++ 是对 Hydra 的改进,它在 Hydra 基础上,引入了一个新的 Hydra Head 结构,这个 Hydra Head 可以同时处理多个候选序列,从而进一步提升了整体的推理速度。
- 在hydra heads推理中,为输入序列添加噪声;将每个头部的MLP扩展为4层。
- 为了增强草稿模型利用整个上下文信息(而不仅仅是最近验证过的token)的能力,在基础模型中添加了一个额外的自注意力解码层。这一新增的层在每个decoding step中仅被query一次。
Draft & Verify
这个方法在起草阶段同样使用大模型进行推理,但是选择性地跳过一些层,起到将大模型作为小草稿模型来使用的效果。因此本文需要解决两个问题:
- 如何确定在起草过程中要跳过的层和层数
作者将其表述为一个贝叶斯优化问题,它接收要绕过的层组合作为输入,目标是最大限度地减少每个 token 的平均推理时间。目标函数为:
\[z^* = \arg\min_{z} f(z), \quad \text{s.t. } z \in \{0, 1\}^L.\]- 如何决定停止生成 draft tokens 的时间
可以在置信度分数低于某个预定义的静态阈值时停止生成 draft tokens 。关于如何设置这个阈值,本文提出了一种自适应阈值更新方法,该阈值会根据更新规则动态调整,从而可以准确反映大模型接受率并更好地处理不同难度的输入样本:
\[\begin{align} AR &\leftarrow \beta_1 AR + (1 - \beta_1) AR_e, \\ \tilde{\gamma} &= \begin{cases} \gamma + \epsilon, & \text{if } AR \leq \alpha, \\ \gamma - \epsilon, & \text{otherwise}, \end{cases} \\ \gamma &\leftarrow \beta_2 \gamma + (1 - \beta_2) \tilde{\gamma}. \end{align}\]其中 $\alpha$ 是大模型接受率, $\epsilon$ 是更新步长,$\beta_1$ 和 $\beta_2$ 是用于减小 \(\gamma\) (生成草稿长度) 和表示自回归波动的因子。在每个验证阶段后更新\(\gamma\) 。这种更新规则确保接受率保持在接近大模型接受率 $\alpha$ 的范围内。
Lookahead Decoding
Jacobi Decoding
本文受到 Accelerating Transformer Inference for Translation via Parallel Decoding 的启发,这篇工作提出了一种将 llm 的自回归解码转换为可并行求解的非线性方程组的方法,称为 Jacobi Decoding,它使用固定点 Jacobi 迭代方法来实现并行化解码。
具体来说,Jacobi Decoding 将顺序解码过程重新表述为一个由 n 个变量组成的非线性方程组,并基于雅可比迭代并行求解:
\[f(y_i, y_{-i}; \mathbf{x}) = 0 \quad \text{for} \quad i = 1, \ldots, n \implies \begin{cases} y_1^{(j+1)} = \arg \max_y \, p(y \mid \mathbf{x}) \\ y_2^{(j+1)} = \arg \max_y \, p(y \mid y_1^{(j)}, \mathbf{x}) \\ \vdots \\ y_n^{(j+1)} = \arg \max_y \, p(y \mid y_{1:n}^{(j)}, \mathbf{x}) \end{cases}\]其中,$y_1,y_2,…,y_n$ 表示模型生成的序列的各个位置上的 token。每个迭代步骤可能会预测多个正确的tokens(“正确”是指与贪婪采样策略下的自回归解码结果对齐),从而实现并行化解码。 然而,在实践中,原始的 Jacobi Decoding 方法的加速比很小。这是因为当前一个 token 错误时,LLM 很少能生成下一个正确的 token;同时,大模型很难在一次迭代中同时实现对多个 token 的准确解码和定位。
Jacobi Trajectory
在上述Jacobi Decoding 的目标方程组中,$\mathcal{J} := {\mathbf{y}^{(1)}, \ldots, \mathbf{y}^{(k)}}$ 称为雅可比轨迹(Jacobi Trajectory)。雅可比轨迹代表了模型在生成文本时,通过并行优化每个解码位置的预测结果逐渐逼近最终输出的过程。 当 $y(j+1)=y(j)$ 时,解码过程收敛,最终固定点 $y$ 即为模型解码输出。雅可比轨迹为理解解码的收敛性提供了直观解释,通过分析轨迹,可以评估解码的效率(需要多少次迭代达到收敛)以及模型的稳定性(是否总能收敛到合理的结果)。 例如,假设我们使用雅可比解码生成一句话,初始预测为随机的 token $\mathbf{y}^{(1)}$ ,第一轮预测输出一些不连贯的文本。随着迭代次数增加 $(\mathbf{y}^{(2)},\mathbf{y}^{(3)})$,每个位置的 token 都会基于更准确的上下文被逐步修正,直到得到连贯的句子作为固定点 $y$ 。这一修正和优化过程便是雅可比轨迹的现实体现。 总之,雅可比轨迹展示了通过并行更新逐步逼近最终解码结果的过程,反映了 LLM 的解码机制从局部优化走向整体稳定的动态变化。
Lookahead Decoding
本文注意到在 Jacobi Decoding 中,单个位置的每个新 token 都是根据之前迭代的历史值进行解码的,这会在每个 token 的位置创建历史标记的轨迹,形成许多n-gram。例如,通过 3 次 Jacobi iterations,可以在每个 token 位置形成 3-gram。Lookahead decoding 通过从雅可比轨迹(Jacobi trajectory)中收集和缓存这些 n-grams,并将它们作为草稿。同时,维护一个 n-gram pool 来缓存历史生成的 n-gram。
Lookahead decoding 使用雅可比迭代对未来 tokens 执行并行解码,还同时验证 cache 中有可能选中的 n-gram 模型。接受 N-gram 允许我们一步推进 N 个标记,从而加速解码过程,如下图:
每个解码步骤都分为两个并行分支:lookahead branch 和 verification branch。
- lookahead branch 维护一个固定大小的 2D 窗口,以根据雅可比迭代轨迹生成 n-gram。
- verification branch 选择并验证有前途的 n-gram 候选序列。
通过检索生成draft
REST
REST: Retrieval-Based Speculative Decoding 是一种基于字符串检索的推测解码方法,可以与任何llm无缝集成。作者在 HumanEval 和 MT-Bench 上做了实验,可以达到不错的效果
在推理过程中,输入上下文用作query,并从数据存储中检索与输入的最长后缀匹配的文档,然后使用检索到的文档中的 continuation 构建 Trie前缀树。我们修剪低频(权重)分支,剩余的子树进一步用作推测解码中的draft tokens。 draft tokens 被输入到 LLM 中,并使用 tree attention mask 进行验证。
检索数据库的过程是在 cpu 上进行的,这意味着在推测解码的过程中要不断地往返于 host 和 device 之间;每增加一个数据集就需要在磁盘上维护一个相应的巨大数据库,同时也可能会使小草稿模型只具备在特定的数据集上快速生成草稿的能力。
for span_id, token_span in enumerate(token_spans):
this_token = input_ids_extend.squeeze(0)[-token_span:].to("cpu").tolist()
# Retrieve draft tokens from the datastore, and get draft buffer
retrieved_token_list, _draft_attn_mask, _tree_indices, _draft_position_ids, _retrieve_indices = datastore.search(this_token, choices=max_num_draft)
Prompt Lookup Decoding
这个工作简单而有效,目前已经集成自transformers库,可以直接调用。它的优势在于不需要额外训练和外部数据库,同样是一种基于字符串检索的方法,但是应用场景有限。
这篇文章基于一个假设:当 llm 进行一些依赖输入prompt的下游任务(如摘要、文档问答、多轮对话、代码编辑)时,这些任务的输入 prompt 和输出之间存在高度的 n-gram重叠,因此大模型可以在生成输出时直接从输入中查找这些内容。
class PromptLookupCandidateGenerator(CandidateGenerator)
代码的核心部分是通过 n-gram 匹配 从输入中提取可能的候选序列:
for ngram_size in range(min(self.max_matching_ngram_size, input_length - 1), 0, -1):
# 使用滑动窗口 (unfold) 在输入序列中生成 n-gram
windows = input_ids.unfold(dimension=1, size=ngram_size, step=1)
# 提取输入序列末尾的 n-gram
ngram_tensor = input_ids[0, -ngram_size:]
# 对比滑动窗口中的 n-gram,与末尾的 n-gram 匹配
matches = (windows == ngram_tensor).all(dim=2)
# 找到匹配的索引 match_indices
match_indices = matches.nonzero(as_tuple=True)[1]
基于匹配的索引 match_indices 生成候选序列,并将候选序列存储在 chosen_ids 中:
for idx in match_indices:
start_idx = idx + ngram_size
end_idx = start_idx + self.num_output_tokens
end_idx = min(end_idx, input_length, self.max_length)
if start_idx < end_idx:
chosen_ids = input_ids[0, start_idx:end_idx]
match_found = True
如果未找到匹配的 n-gram,就返回当前输入序列,使用传统的自回归解码。最后将候选序列与输入序列使用 torch.cat 拼接,return 给验证阶段。
与稀疏 KV Cache 结合
MagicDec
MagicDec: Breaking the Latency-Throughput Tradeoff for Long Context Generation with Speculative Decoding
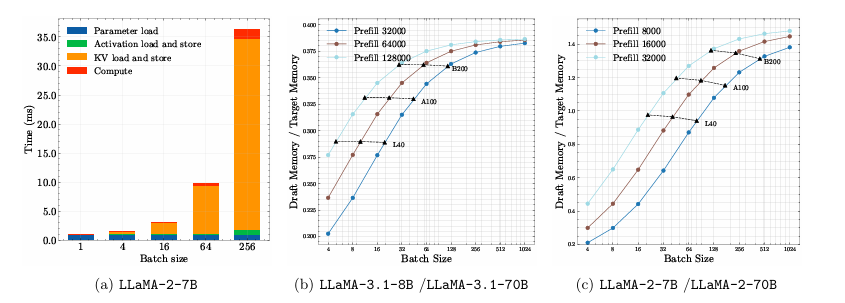
这篇文章探讨了将推测解码与稀疏 KV Cache 结合的可能性。作者做了一些实验,并认为在大 batch size 的情况下,实际限制 throughput 的并非小模型的推理时间或者大模型的验证时间,而是小模型 KV Cache 的加载时间。
因此本文的核心思想是:既然随着 batch size 的增大,影响 throughput 的主要瓶颈变为 KV Cache 的读取,那么我们就使用一个具有稀疏 KV Cache 的小草稿模型,这个小草稿模型在每一时刻的 KV Cache 都是恒定不变的。
这篇文章也注意到推测解码在批量验证时的限制,但并没有从本质上修改每个sequence的验证逻辑或注意力内核,而是做了一些实验来表明如何通过kv cache稀疏化的方法提升批处理时小模型的推理速度。
尽管推测解码对于单样本请求很有希望,但在实现批处理支持时会带来新的挑战。由于推测解码中接受的 tokens 数量遵循截断的几何分布(见 Leviathan 等),因此平均接受长度可能会在整个批次中发生变化,从而导致整个 batch 的序列长度不一致。Bass(Batched attention-optimized speculative sampling)优化了注意力 kernel,以处理一个 batch 中接受的 tokens 数量不等的情况。然而,推测解码的过量计算可能会在大 batch size 的情况下受到限制。
疑问:这会不会导致草稿模型的推理性能减弱,草稿接受率更低?
The fixed draft KV budget naturally raises concern about the acceptance rate, which is another important deciding factor. Fortunately, StreamingLLM with a small KV budget like 512 is able to retain a high acceptance rate even for sequences as long as 100K! To further improve the acceptance rate, we can increase the drafting budget in different ways as long as the draft to target cost ratio remains reasonably small.
这篇文章并没有提出一个自己的模型或算法,更多的是展示实验结果,并选了一些外部的 kv cache 压缩方法直接拿来用(与小草稿模型集成)。作者选的是SnapKV 和 StreamingLLM。
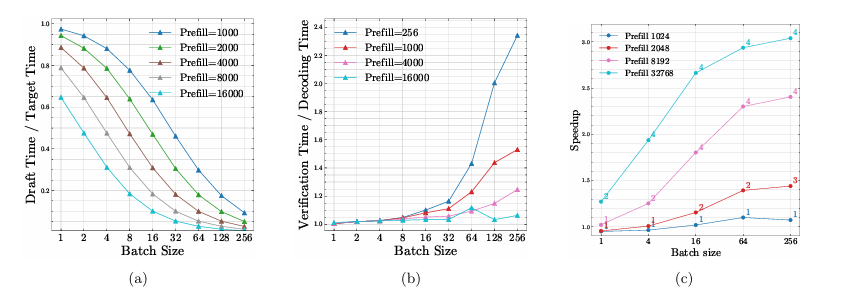
正确性与一致性(非贪婪采样)
当我们把贪婪解码切换为温度采样、Top‑k 或核采样(Top‑p)时,推测解码的“验证”不再等同于重放单一路径。要保持分布一致,核心是让接受规则与目标抽样等价:起草阶段从近似分布 q 生成候选,验证阶段依据目标分布 p 的 logits 逐位校验;若候选与 p 下的采样结果一致,则整段接受,否则立即回退到用 p 抽样该位并丢弃剩余草稿。这个过程本质上是逐位的拒绝采样,可在理论上保证与目标采样过程一致。工程上,典型接受(Typical Acceptance)会用“典型性/熵阈值”等准则放宽校验以提高通过率,但需用困惑度、任务指标与人评持续回归,避免质量漂移;对代码、医疗等高风险域建议固定为严格一致。另一个容易忽视的细节是随机性:应将草稿与验证的随机流分离并记录温度、种子、Top‑k/Top‑p 等参数到日志,确保可审计与可复现。
批处理与调度
在真实服务中,请求以批为单位进入系统。由于“单步可接受长度”服从截断的几何分布,其方差会导致批内步幅不同步,出现“头阻塞”:快样本空等慢样本。实践上可以从两端发力:其一,对批内样本做轻量整形,让草稿深度更接近(长度分桶、动态 padding),并在时间维度采用连续批处理(continuous batching)滚动并入新请求,减少空转;其二,根据实时接受率的指数滑动均值与显存水位,自适应调整 micro‑batch 大小与步幅,平衡吞吐与时延。调度层建议区分 SLA 建立分级队列,并为每个批次记录接受长度分布、丢弃比例与 P50/P95 时延。这样既能发现“长尾”样本拖慢全批的问题,也方便做有损/有界时延的权衡策略。
KV Cache 管理细节
树状起草与验证会在同一上下文上分出多条候选路径;若 KV Cache 管理不当,很容易触发大规模拷贝与碎片化,直接拖慢带宽。一个通用准则是“共享前缀,惰性物化”:分支尽量共享祖先 KV,只有在某条分支被真正接受并继续前推时才进行写时复制(copy‑on‑write)。为此,建议使用页式/池化分配器统一 KV 块尺寸与步幅,降低碎片;配合分层账本分别统计 context/草稿/验证占用,并设置高水位触发回收与轻量整理。长上下文场景可以结合稀疏或压缩 KV(如 SnapKV、StreamingLLM)以减少读写放大与 PCIe 传输。实现层面要特别注意两点:其一,树验证必须使用“仅可见祖先”的注意力掩码与位置编码(RoPE)对齐,避免跨分支“看见兄弟”;其二,优先使用异步内存接口(如 cudaMallocAsync)与流内事件,减少分配/回收的同步抖动。
框架生态与落地清单
在已有生态中,vLLM 提供了推测采样与 Prompt Lookup 的实现,易与连续批处理和分页式 KV 管理协同;TensorRT‑LLM 在 Medusa/Hydra 一类的树式验证上做了较深的内核融合与图优化,适合追求极致吞吐的在线/离线部署;Transformers 更适合研究与原型,工程化时通常需要联用 vLLM/Triton 后端以获得稳定的吞吐与时延。落地建议是先用“接受率 × 起草速度 × 验证成本”的乘积构建 A/B 基线,再上线可观测看板,持续跟踪接受率分布、草稿深度、验证利用率、端到端吞吐/时延与质量回退率。对高风险域默认启用严格一致并配自动回退,同时把起草/验证规则、随机种子与版本固化到文档与日志,保证复现与审计。
Reference
- Speculative Decoding: Exploiting Speculative Execution for Accelerating Seq2seq Generation
- Fast Inference from Transformers via Speculative Decoding, Yaniv Leviathan et al., 2023
- Accelerating Large Language Model Decoding with Speculative Sampling, Charlie Chen et al., 2023
- Eagle
- Accelerating Transformer Inference for Translation via Parallel Decoding
- MagicDec: Breaking the Latency-Throughput Tradeoff for Long Context Generation with Speculative Decoding
